
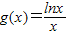 ,它们的定义域都是(0,e],其中e≈2.718,a∈R
,它们的定义域都是(0,e],其中e≈2.718,a∈R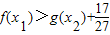
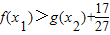 成立,只需要求出函数f(x)的最小值,与函数
成立,只需要求出函数f(x)的最小值,与函数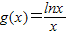 的最大值,用函数f(x)的最小值减去函数
的最大值,用函数f(x)的最小值减去函数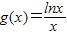 的最大值令它们的差与
的最大值令它们的差与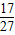 比较即可,
比较即可,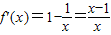
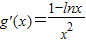 g'(x)≥0在区间(0,e]上成立
g'(x)≥0在区间(0,e]上成立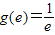
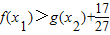
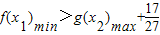
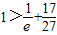 ,即证e>2.7
,即证e>2.7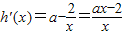
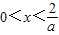
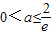 时,
时,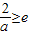 ,
,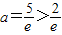 ,舍去
,舍去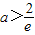 时,
时,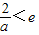 ,
,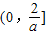 单调递减,在
单调递减,在 单调递增,
单调递增,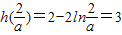 ,
,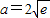 ,满足要求
,满足要求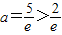 ,舍去
,舍去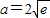
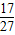 ,第三问中令最小值等于3建立方程求参数的值,转化化归是数学中的一个重要数学思想,在高中数学解题中经常用到,要注意此思想在本题中应用方法与规律,作为以后解题的借鉴.本题中也用到了分类讨论的思想,由此本题思维含量大,运算量大,解题难度较大,求解时要认真严谨,莫因马虎致错.
,第三问中令最小值等于3建立方程求参数的值,转化化归是数学中的一个重要数学思想,在高中数学解题中经常用到,要注意此思想在本题中应用方法与规律,作为以后解题的借鉴.本题中也用到了分类讨论的思想,由此本题思维含量大,运算量大,解题难度较大,求解时要认真严谨,莫因马虎致错. 

 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案科目:高中数学 来源: 题型:
| a-x2 |
| x |
| 1 |
| 2 |
| 1 |
| 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com