
����Ŀ��ij���ڴ���ȫ�����γ��еĻ��,��һ����OΪԲ��,R(RΪ����,��λ:��)Ϊ�뾶�İ�Բ�λĵؽ�����������,���й���BCD����(��Ӱ����)��ֲ��ƺ,��OBD�������ڶ�ͯ������,��������������ֲ����ֲ��.��֪��ֲ��ƺ����ֲ��ijɱ��ֱ���ÿƽ����5Ԫ��55Ԫ,��ͯ�������������ÿƽ����95Ԫ.
(1)���BOD=��(��λ:����),������ʾ����BCD�����S��=f(��).
(2)������й滮��������滮�������,�����ơ�BOD�Ĵ�С����ʹ���������?��������ֵ.

���𰸡���1��S��=f(��)= ![]() R2(��-sin ��),����(0,��).��2��������
R2(��-sin ��),����(0,��).��2��������
��������
��1����S��=S����S�����������μ������������ʽ���ã�
��2���������г�������ϵʽ�����õ����жϺ���������������ֵ���ɣ�
��: ��1��S��=![]() R2�ȣ�S��OBD=
R2�ȣ�S��OBD=![]() R2sin�ȣ�
R2sin�ȣ�
S��=f���ȣ�=![]() R2���ȩ�sin�ȣ����ȡʣ�0���У�
R2���ȩ�sin�ȣ����ȡʣ�0���У�
��2����������ΪyԪ����ͯ������Ϊy1Ԫ����ֲ��ƺ�ɱ�Ϊy2Ԫ����ֲ����ֲ��ɱ�Ϊy3Ԫ��
��y1=![]() R2sin��95��y2=
R2sin��95��y2=![]() R2���ȩ�sin�ȣ�5��y3=
R2���ȩ�sin�ȣ�5��y3=![]() R2���Щ��ȣ�55��
R2���Щ��ȣ�55��
��y=y1��y2��y3=![]() R2��100sin��+50�ȩ�55�У���
R2��100sin��+50�ȩ�55�У���
��g���ȣ�=100sin��+50�ȩ�55�У��ȡʣ�0���У���
��g�䣨�ȣ�=100cos��+50
��g�䣨�ȣ�>0��cos�ȣ���![]() ��g���ȣ��ڦ��ʣ�0��
��g���ȣ��ڦ��ʣ�0��![]() ����Ϊ��������
������������
g�䣨�ȣ�<0��cos�ȣ���![]() ��g���ȣ��ڦ��ʣ�
��g���ȣ��ڦ��ʣ�![]() ���У���Ϊ��������
���У���Ϊ��������
����=![]() ʱ��g���ȣ�ȡ�����ֵ����ʱ���������
ʱ��g���ȣ�ȡ�����ֵ����ʱ���������
��ʱ���������y=![]() R2��100sin��+50�ȩ�55�У�=
R2��100sin��+50�ȩ�55�У�=![]() R2��50
R2��50![]() ��
��![]() ����
����
�����Ե��ֹ�˾�����ε�Բ�Ľ���Ƴ�ʱ��������ȡ���ֵ![]() R2��50
R2��50![]() ��
��![]() ��
�У�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ����
����![]() ʱ������
ʱ������![]() ������
������
![]() ��a��ֵ��
��a��ֵ��
![]() �жϲ�֤������
�жϲ�֤������![]() �ĵ����ԣ�
�ĵ����ԣ�
![]() ��
��![]() ��
��![]() �ϵ�ֵ��
�ϵ�ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���±��ṩ��ij�����ܽ��ļ�������������ײ�Ʒ�����м�¼�IJ���![]() ���֣�����Ӧ�������ܺ�
���֣�����Ӧ�������ܺ�![]() ���֣���ú�ļ���������ݣ�
���֣���ú�ļ���������ݣ�
| 3 | 4 | 5 | 6 |
| 2.5 | 3 | 4 | 4.5 |
��1��������ϱ��ṩ�����ݣ�����С���˷����![]() ����
����![]() �����Իع鷽��
�����Իع鷽��![]() ��
��
��2����֪�ó���������ǰ100�ּײ�Ʒ�ܺ�Ϊ90�ֱ�ú���Ը��ݣ�1����������Իع鷽�̣�Ԥ������100�ּײ�Ʒ�������ܺıȼ�������ǰ���Ͷ��ٶֱ�ú��
����� ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������ĸ����⣺
�ٺ���y= ![]() Ϊ�溯����
Ϊ�溯����
��y=2 ![]() ��ֵ���ǣ�1��+�ޣ�
��ֵ���ǣ�1��+�ޣ�
�ۺ���y= ![]() �ڶ��������Ǽ�������
�ڶ��������Ǽ�������
��������f��2x���Ķ�����Ϊ[1��2]������y=f�� ![]() ��������Ϊ[4��8]
��������Ϊ[4��8]
������ȷ���������� �� ������������ȷ�������ţ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ���ǵ�Բ����ˮͰ����Ҫʹ�������![]() ����������ʡ����Բ���ĵ���뾶Ϊ__________��
����������ʡ����Բ���ĵ���뾶Ϊ__________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������ABCA1B1C1�������ⳤ��Ϊ2��DΪCC1���е㣮

(1)��֤��AB1��ƽ��A1BD��
(2)������AA1DB������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=Asin����x+����A��0���أ�0��||�� ![]() �����䵼����f'��x���IJ���ͼ����ͼ��ʾ������f��x���Ľ���ʽΪ�� ��
�����䵼����f'��x���IJ���ͼ����ͼ��ʾ������f��x���Ľ���ʽΪ�� �� 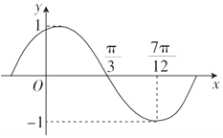
A.![]()
B.![]()
C.![]()
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������{an}��{bn}��SnΪ����{an}��ǰn��ͣ���Sn+1����n+1��=Sn+an+n��a1=b1=1��bn+1=3bn+2��n��N* ��
��1��������{an}��{bn}��ͨ�ʽ��
��2����cn= ![]() ��������{cn}��ǰn���Tn ��
��������{cn}��ǰn���Tn ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ں���f��x���������ڳ���a��0��ʹ��xȡ�������ڵ�ÿһ��ֵ������f��x��=��f��2a��x�������f��x��Ϊ���溯�������������к�������f��x��= ![]() ����f��x��=��x+1��2����f��x��=x3����f��x��=sin��x+1�������еġ��溯��������д�����С��溯��������ţ�
����f��x��=��x+1��2����f��x��=x3����f��x��=sin��x+1�������еġ��溯��������д�����С��溯��������ţ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com