Question

设f(k)是满足不等式log₂x+log₂(3×2^k-1-x)≥2k-1(k∈N₊)的自然数x的个数.

(1)求f(k)的解析式；

（2）记S_n=f(1)+f(2)+…+f(n)，求S_n的解析式；

（3）令P_n=n²+n-1(n∈N₊),试比较S_n与P_n的大小.

Answer 1

解：(1)由已知不等式可得

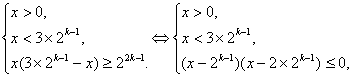
2^k-1≤x≤2^k,从而f(k)=2^k-2^k-1+1=2^k-1+1.

(2)S_n=f(1)+f(2)+…+f(n)

=2⁰+2¹+…+2^n-1+n

=2ⁿ+n-1.

(3)S_n-P_n=2ⁿ-n².

当n=1时,2¹-1²＞0;当n=2时,2²-2²=0;

当n=3时,2³-3²＜0;当n=4时,2⁴-4²=0;

当n=5时,2⁵-5²＞0;当n=6时,2⁶-6²＞0.

猜想：当n≥5时,S_n＞P_n.

下面用数学归纳法证明：

①当n=5时,S_n＞P_n,上面已证；

②假设n=k时，S_k＞P_k,即2^k＞k²,

则n=k+1时,

∵S_k-P_k+1=2^k+1-(k-1)²＞2k²-(k+1)²=(k-1)²-2,

当k≥5时，(k-1)²-2＞0,∴S_k+1＞P_k+1.

故当n≥5时，总有S_n＞P_n成立.

综上可知：当n=1或n≥5时，有S_n＞P_n;

当n=2或n=4时,S_n=P_n;

当n=3时,S_n＜P_n.