
【题目】已知椭圆![]()
![]() 的焦距为2,离心率为
的焦距为2,离心率为![]() ,
,![]() 轴上一点
轴上一点![]() 的坐标为
的坐标为![]() .
.
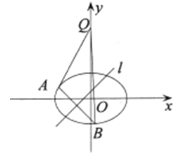
(Ⅰ)求该椭圆的方程;
(Ⅱ)若对于直线![]() ,椭圆
,椭圆![]() 上总存在不同的两点
上总存在不同的两点![]() 与
与![]() 关于直线
关于直线![]() 对称,且
对称,且![]() ,求
,求
实数![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() .
.
【解析】
试题分析:(Ⅰ)由已知易得![]() ,
,![]() ;(Ⅱ)由已知当椭圆
;(Ⅱ)由已知当椭圆![]() 上总存在不同的两点
上总存在不同的两点![]() 与
与![]() 关于直线
关于直线![]() 对称时,取弦
对称时,取弦![]() 中点
中点![]() ,由中点弦问题可知
,由中点弦问题可知![]() ,又
,又![]() ,可得
,可得![]() ,由
,由![]() 在椭圆内,故
在椭圆内,故![]() ,即
,即![]() ,又联立
,又联立![]() ,得
,得![]() ,
,![]() ,得
,得![]() ,所以
,所以![]() 的取值范围为
的取值范围为![]() .
.
试题解析:(Ⅰ)由题意知:![]() ,
,![]() ,所以
,所以![]() ,
,![]() .
.
所以所求的椭圆的方程为![]() .
.
(Ⅱ)由题意设![]() ,
,![]() ,直线
,直线![]() 方程为:
方程为:![]() .
.
联立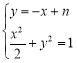 消
消![]() 整理可得:
整理可得:![]() ,
,
由![]() ,解得
,解得![]()
![]() ,
,![]() ,
,
设直线![]() 之中点为
之中点为![]() ,则
,则![]() ,
,
由点![]() 在直线
在直线![]() 上得:
上得:![]() ,
,
又点![]() 在直线
在直线![]() 上,
上,![]() ,所以
,所以![]() ……①
……①
又![]() ,
,![]() ,
,
∴![]()
![]()
![]()
![]()
![]()
解得:![]() ……②
……②
综合①②,![]() 的取值范围为
的取值范围为![]() .
.
(法二:请酌情给分)
由题意设![]() ,
,![]() ,直线
,直线![]() 的中点为
的中点为![]() ,
,
则![]() ,
,
将![]() ,
,![]() 两点分别代入椭圆方程,
两点分别代入椭圆方程,
并联立![]() ,两式相减得:
,两式相减得:![]() ,
,
即![]() ,
,
又![]() ,所以,
,所以,![]() ,
,
所以,![]() 的中点
的中点![]() 的轨迹方程为:
的轨迹方程为:![]() ,
,
由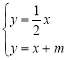 得:
得:![]() ,即
,即![]() ,
,
又∵![]() 在椭圆内,∴
在椭圆内,∴![]() ,即
,即![]() ,
,
即![]() ,①
,①
另一方面:易知:直线![]() 的方程
的方程![]() ;
;
联立![]() ,消去
,消去![]() 并整理得:
并整理得:![]() ,
,
∴![]() ,
,![]() ,
,
又![]() ,
,![]() ,
,
∴![]()
![]()
![]()
![]()
![]()
解得:![]() ,②
,②
综合①②:![]() 的取值范围为
的取值范围为![]()


科目:高中数学 来源: 题型:
【题目】某公司生产一批![]() 产品需要原材料500吨,每吨原材料可创造利润12万元,该公司通过设备升级,生产这批
产品需要原材料500吨,每吨原材料可创造利润12万元,该公司通过设备升级,生产这批![]() 产品所需原材料减少了
产品所需原材料减少了![]() 吨,且每吨原材料创造的利润提高了
吨,且每吨原材料创造的利润提高了![]() ;若将少用的
;若将少用的![]() 吨原材料全部用于生产公司新开发的
吨原材料全部用于生产公司新开发的![]() 产品,每吨原材料创造的利润为
产品,每吨原材料创造的利润为![]() 万元,其中
万元,其中![]() .
.
(1)若设备升级后生产这批![]() 产品的利润不低于原来生产该批
产品的利润不低于原来生产该批![]() 产品的利润,求
产品的利润,求![]() 的取值范围;
的取值范围;
(2)若生产这批![]() 产品的利润始终不高于设备升级后生产这批
产品的利润始终不高于设备升级后生产这批![]() 产品的利润,求
产品的利润,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法中错误的是_______(填序号)
①命题“![]() 有
有![]() ”的否定是“
”的否定是“![]() 有
有![]() ”;
”;
②若一个命题的逆命题为真命题,则它的否命题也一定为真命题;
③已知![]() ,
, ![]() ,若命题
,若命题![]() 为真命题,则
为真命题,则![]() 的取值范围是
的取值范围是![]() ;
;
④“![]() ”是“
”是“![]() ”成立的充分条件.
”成立的充分条件.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】命题p:关于x的方程x2+ax+2=0无实根,命题q:函数f(x)=logax在(0,+∞)上单调递增,若“p∧q”为假命题,“p∨q”真命题,求实数a的取值范围
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某河上有座抛物线型拱桥,当水面距拱顶5m时水面宽为8m,一木船宽为4m,高为2m,载货后木船露在水面上的部分高为0.75m,问水面上涨到与拱顶相距多少时,木船开始不能通过。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一个盒子里装有6张卡片,上面分别写着如下定义域为![]() 的函数:
的函数:
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
(1)现在从盒子中任意取两张卡片,记事件![]() 为“这两张卡片上函数相加,所得新函数是奇函数”,求事件
为“这两张卡片上函数相加,所得新函数是奇函数”,求事件![]() 的概率;
的概率;
(2)从盒中不放回逐一抽取卡片,若取到一张卡片上的函数是偶函数则停止抽取,否则继续进行,记停止时抽取次数为![]() ,写出
,写出![]() 的分布列,并求其数学期望
的分布列,并求其数学期望![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com