
若![]() ,
,![]() ,x∈R,p1,p2为常数,且
,x∈R,p1,p2为常数,且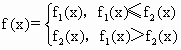
(1)求f(x)=f1(x)对所有实数x成立的充要条件(用p1,p2表示)
(2)设a,b为两实数,a<b且p1,p2∈(a,b)若f(a)=f(b)
求证:f(x)在区间[a,b]上的单调增区间的长度和为![]() (闭区间[m,n]的长度定义为n-m)
(闭区间[m,n]的长度定义为n-m)
|
本小题考查充要条件、指数函数于绝对值函数、不等式的综合运用. (1) 若 当 所以 当 所以 综上所述, (2)10如果 因为 因为减区间为 20如果 于是当 当 当 由方程 显然 所以 综上可知,在区间 故由函数 故由(1)(2)得 综合1020可知,
|


科目:高中数学 来源: 题型:
|
| b-a |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
|
| b-a |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 4x+2 |
| 1 |
| 2 |
| n |
| m |
| am |
| Sm |
| am+1 |
| Sm+1 |
查看答案和解析>>
科目:高中数学 来源:2011-2012学年黑龙江省哈尔滨三中高一(上)期末数学试卷(解析版) 题型:解答题
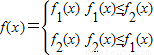
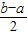 .(区间[m,n]、(m,n)或(m,n]的长度均定义为n-m)
.(区间[m,n]、(m,n)或(m,n]的长度均定义为n-m)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com