
(12分)设等比数列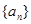 的前
的前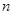 项和为
项和为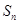 ,已知
,已知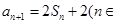 N
N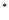 ).
).
(1)求数列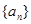 的通项公式;(6分)
的通项公式;(6分)
(2)在 与
与 之间插入n个数,使这n+2个数组成公差为
之间插入n个数,使这n+2个数组成公差为 的等差数列,求数列
的等差数列,求数列 的前
的前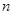 项和
项和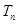 .(6分)
.(6分)
(1)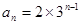 ;(2)
;(2)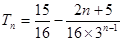 。
。
【解析】(1) 由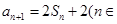 Z*),得
Z*),得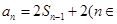 Z*,
Z*,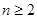 ),
),
再两式相减得: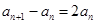 ,从而可得
,从而可得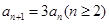 ,又因为
,又因为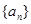 是等比数列,所以
是等比数列,所以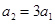 ,从而求出首项a1,得到
,从而求出首项a1,得到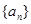 的通项公式.
的通项公式.
(2) 由(1)知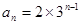 ,则
,则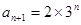 ,又∵
,又∵ ,从而可得
,从而可得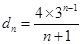 ,所以
,所以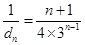 ,所以采用错位相减的方法求和即可.
,所以采用错位相减的方法求和即可.
(1)由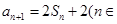 Z*)
Z*)
得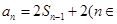 Z*,
Z*,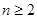 ),………………………………2分
),………………………………2分
两式相减得: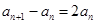 ,
,
即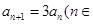 Z*,
Z*,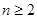 ),………………………………4分
),………………………………4分
∵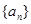 是等比数列,所以
是等比数列,所以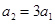 ; 又
; 又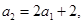 则
则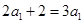 ,∴
,∴ ,
,
∴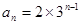 …………………………6分
…………………………6分
(2)由(1)知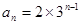 ,则
,则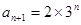
∵ ,
,
∴ …………………8分
…………………8分
∵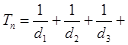 …
…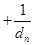
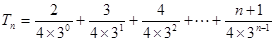 ①
①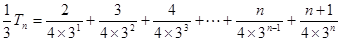 ②…………………10分
②…………………10分
①-②得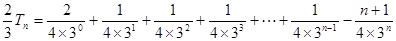
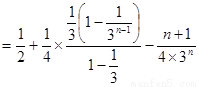
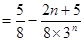 ……………………………………11分
……………………………………11分
∴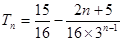 ……………………………………12分
……………………………………12分


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案科目:高中数学 来源:2010-2011学年北京市西城区高三第一学期期末考试数学理卷 题型:选择题
设等比数列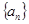 的前
的前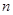 项和为
项和为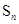 ,若
,若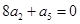 ,则下列式子中数值不能确定的是
,则下列式子中数值不能确定的是
(A)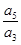 (B)
(B)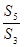 (C)
(C)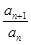 (D)
(D)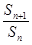
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com