
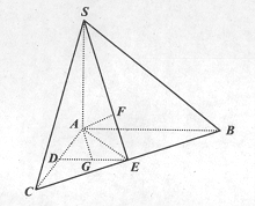
【题目】如图,在三棱锥S-ABC中,SA ⊥底面ABC,AC=AB=SA=2,AC ⊥AB,D,E分别是AC,BC的中点,F在SE上,且SF=2FE.
(Ⅰ)求异面直线AF与DE所成角的余弦值;
(Ⅱ)求证:AF⊥平面SBC;
(Ⅲ)设G为线段DE的中点,求直线AG与平面SBC所成角的余弦值。
【答案】(Ⅰ)![]() ;(Ⅱ)详见解析;(Ⅲ)
;(Ⅱ)详见解析;(Ⅲ)![]() .
.
【解析】
(Ⅰ)由题意可知DE∥AB,故∠FAB或其补角为异面直线AF与DE所成角;
(Ⅱ)由(I)知AF⊥SE,易证BC⊥AF,从而AF⊥平面SBC;
(Ⅲ)延长AG交BC于P点,连结PF. 由(II)知AF⊥平面SBC,所以PF为AP在平面SBC上的投影,故∠APF即为直线AG与平面SBC所成角
解(I).连结BF.

在△ABC中,D,E分别是AC,BC的中点,
∴DE∥AB,
∴∠FAB或其补角为异面直线AF与DE所成角
由AC=AB=SA=2,AC⊥AB,E是BC的中点,得AE=![]()
∵SA⊥底面ABC,∴SA⊥AE.
在Rt△SAE中,SE=![]() ,可得
,可得![]()
∵SA⊥底面ABC,∴.SA⊥BC,又BC⊥AE,
∴BC⊥平面SAE,
∴BC⊥SE,
∵![]()
∴BF=![]()
∴![]()
即异面直线AF与DE所成角的余弦值![]() 。
。
(II).由(I)知![]() ,∴AF⊥SE.
,∴AF⊥SE.
∵BC⊥平面SAE,所以BC⊥AF.
又SE![]() BC=E,.AF⊥平面SBC.
BC=E,.AF⊥平面SBC.
(III).延长AG交BC于P点,连结PF.
由(II)知AF⊥平面SBC,∴PF为AP在平面SBC上的投影,
∴∠APF即为直线AG与平面SBC所成角
∵G为线段DE的中点,
∴CP=2PE,又SF=2FE,
.∴![]()
![]() ,
,
即直线AG与平面SBC所成角的余弦值为![]()


 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() (a,b为常数),
(a,b为常数),
(1)当![]() 时,求函数
时,求函数![]() 的单调区间;
的单调区间;
(2)在(1)的条件下,![]() 有两个不相等的实根,求b的取值范围;
有两个不相等的实根,求b的取值范围;
(3)若对任意的![]() ,不等式
,不等式![]() 在
在![]() 上恒成立,求b的取值范围.
上恒成立,求b的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)
某市为增强市民的环境保护意识,面向全市征召义务宣传志愿者.现从符合条件的志愿者中随机抽取100名按年龄分组:第1组![]() ,第2组
,第2组![]() ,第3组
,第3组![]() ,第4组
,第4组![]() ,第5组
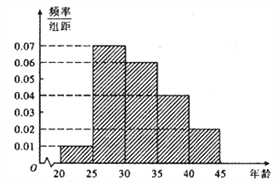
,第5组![]() ,得到的频率分布直方图如图所示.
,得到的频率分布直方图如图所示.
(1)若从第3,4,5组中用分层抽样的方法抽取6名志愿者参广场的宣传活动,应从第3,4,5组各抽取多少名志愿者?
 (2)在(1)的条件下,该县决定在这6名志愿者中随机抽取2名志愿者介绍宣传经验,求第4组至少有一名志愿者被抽中的概率.
(2)在(1)的条件下,该县决定在这6名志愿者中随机抽取2名志愿者介绍宣传经验,求第4组至少有一名志愿者被抽中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 为直角梯形,
为直角梯形,![]() ,
,![]() ,平面
,平面![]() 底面
底面![]() ,
,![]() 为
为![]() 的中点,
的中点,![]() 是棱
是棱![]() 上的点,
上的点,![]() ,
,![]() ,
,![]() .
.
(1)求证:平面![]() 平面
平面![]() ;
;
(2)若![]() 为棱
为棱![]() 的中点,求异面直线
的中点,求异面直线![]() 与
与![]() 所成角的余弦值;
所成角的余弦值;
(3)若二面角![]() 大小为
大小为![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
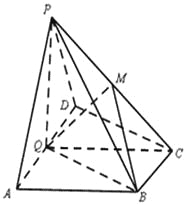
【题目】如图,在四棱锥P﹣ABCD中,PA⊥平面ABCD,底面ABCD是菱形,点O是对角线AC与BD的交点,AB=2,∠BAD=60°,M是PD的中点.

(Ⅰ)求证:OM∥平面PAB;
(Ⅱ)平面PBD⊥平面PAC;
(Ⅲ)当三棱锥C﹣PBD的体积等于 ![]() 时,求PA的长.
时,求PA的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正方体![]() 中,点
中,点![]() ,
,![]() 分别为棱
分别为棱![]() ,
,![]() 的中点,点
的中点,点![]() 为上底面的中心,过
为上底面的中心,过![]() ,
,![]() ,
,![]() 三点的平面把正方体分为两部分,其中含
三点的平面把正方体分为两部分,其中含![]() 的部分为
的部分为![]() ,不含
,不含![]() 的部分为
的部分为![]() ,连结
,连结![]() 和
和![]() 的任一点
的任一点![]() ,设
,设![]() 与平面
与平面![]() 所成角为
所成角为![]() ,则
,则![]() 的最大值为
的最大值为

A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有正整数构成的数表如下:
第一行:1
第二行:12
第三行:1123
第四行:11211234
第五行:1121123112112345
…
第k行:先抄写第1行,接着按原序抄写第2行,然后按原序抄写第3行,…,直至按原序抄写第k﹣1行,最后添上数k.(如第四行,先抄写第一行的数1,接着按原序抄写第二行的数1,2,接着按原序抄写第三行的数1,1,2,3,最后添上数4).将按照上述方式写下的第n个数记作![]() (如
(如![]() ,…),用
,…),用![]() 表示数表第
表示数表第![]() 行的数的个数,求数列{
行的数的个数,求数列{![]() }的前
}的前![]() 项和
项和![]() =____
=____
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com