
已知函数 为偶函数.
为偶函数.
(1)求 的值;
的值;
(2)若方程 有且只有一个根,求实数
有且只有一个根,求实数 的取值范围.
的取值范围.
(1) ;(2)
;(2)  或
或 .
.
解析试题分析:(1)法一:根据 为偶函数,将等式
为偶函数,将等式 化简整理即可得到
化简整理即可得到 的值;法二:根据
的值;法二:根据 为偶函数,得到
为偶函数,得到 即
即 ,从中求解即可得到
,从中求解即可得到 ,检验此时是否满足
,检验此时是否满足 即可;(2)首先将方程
即可;(2)首先将方程 化简:
化简:


 ;由
;由 得
得

 ,进而可得
,进而可得 ,令
,令 ,则*变为关于
,则*变为关于 的方程
的方程 只有一个正实数根,先考虑
只有一个正实数根,先考虑 的情形是否符合,然后针对二次方程的根的分布分该方程有一正一负根、有两个相等的正根进行讨论求解,并保证
的情形是否符合,然后针对二次方程的根的分布分该方程有一正一负根、有两个相等的正根进行讨论求解,并保证 即可,最后根据各种情况讨论的结果写出
即可,最后根据各种情况讨论的结果写出 的取值范围的并集即可.
的取值范围的并集即可.
(1)法一:因为 为偶函数,所以
为偶函数,所以
即
 ,∴
,∴
∴ ,∴
,∴ 6分
6分
法二:因为 为偶函数,所以
为偶函数,所以 即
即 ,解得
,解得
此时 ,
,
 ,所以
,所以 .
.
(2)依题意知: 



∴由 得
得


 8分
8分
令 ,则①变为
,则①变为 ,只需关于
,只需关于 的方程只有一个正根即可满足题意
的方程只有一个正根即可满足题意
(1) 不合题意 9分
不合题意 9分
(2)①式有一正一负根,则 经验证满足
经验证满足 ,
, 11分
11分
(3)若①式有两相等正根,则 ,此时
,此时
若 ,则
,则 ,此时方程
,此时方程 无正根
无正根
故 舍去 13分
舍去 13分
若 ,则
,则 ,且
,且
因此

 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:高中数学 来源: 题型:解答题
已知二次函数 ,
, ,
,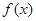 的最小值为
的最小值为 .
.
⑴求函数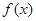 的解析式;
的解析式;
⑵设 ,若
,若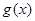 在
在 上是减函数,求实数
上是减函数,求实数 的取值范围;
的取值范围;
⑶设函数 ,若此函数在定义域范围内不存在零点,求实数
,若此函数在定义域范围内不存在零点,求实数 的取值范围.[
的取值范围.[
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
设关于x函数 其中0
其中0
将f(x)的最小值m表示成a的函数m=g(a);
是否存在实数a,使f(x)>0在 上恒成立?
上恒成立?
是否存在实数a,使函数f(x) 在 上单调递增?若存在,写出所有的a组成的集合;若不存在,说明理由.
上单调递增?若存在,写出所有的a组成的集合;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某公司承建扇环面形状的花坛如图所示,该扇环面花坛是由以点 为圆心的两个同心圆弧
为圆心的两个同心圆弧 、弧
、弧 以及两条线段
以及两条线段 和
和 围成的封闭图形.花坛设计周长为30米,其中大圆弧
围成的封闭图形.花坛设计周长为30米,其中大圆弧 所在圆的半径为10米.设小圆弧
所在圆的半径为10米.设小圆弧 所在圆的半径为
所在圆的半径为 米(
米( ),圆心角为
),圆心角为 弧度.
弧度.
(1)求 关于
关于 的函数关系式;
的函数关系式;
(2)在对花坛的边缘进行装饰时,已知两条线段的装饰费用为4元/米,两条弧线部分的装饰费用为9元/米.设花坛的面积与装饰总费用的比为 ,当
,当 为何值时,
为何值时, 取得最大值?
取得最大值?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
学校操场边有一条小沟,沟沿是两条长150米的平行线段,沟宽 为2米,,与沟沿垂直的平面与沟的交线是一段抛物线,抛物线的顶点为
为2米,,与沟沿垂直的平面与沟的交线是一段抛物线,抛物线的顶点为 ,对称轴与地面垂直,沟深2米,沟中水深1米.
,对称轴与地面垂直,沟深2米,沟中水深1米.
(1)求水面宽;
(2)如图1所示形状的几何体称为柱体,已知柱体的体积为底面积乘以高,求沟中的水有多少立方米?

(3)现在学校要把这条水沟改挖(不准填土)成截面为等腰梯形的沟,使沟的底面与地面平行,沟深不变,两腰分别与抛物线相切(如图2),问改挖后的沟底宽为多少米时,所挖的土最少?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
要制作一个如图的框架(单位:m),要求所围成的总面积为19.5(m2),其中ABCD是一个矩形,EFCD是一个等腰梯形,梯形高h= AB,tan∠FED=
AB,tan∠FED= ,设AB=xm,BC=ym.
,设AB=xm,BC=ym.
(1)求y关于x的表达式;
(2)如何设计x、y的长度,才能使所用材料最少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com