
����Ŀ��Ͳ�����ҹ��Ŵ�������һ��ˮ����ȹ��ߣ�������ѧ��������ڡ�ũ��ȫ�顷����ͼ�������Ͳ���Ĺ���ԭ������ͼ1�������侭���ֻ�����������ũҵ�����еõ�ʹ�ã���ͼ2�����ٶ���ˮ�����ȶ�������£�Ͳ���ϵ�ÿһ��ʢˮͲ��������Բ���˶�����Ͳ����ʢˮͲ���˶����������ԣ����Կ����������Ǻ���ģ�Ϳ̻�ʢˮͲ����Ϊ�ʵ㣩���˶����ɣ���Ͳ������Ϊһ������ͼ�Σ�����ֱ������ϵ����ͼ3�����辭��t���Ͳ���ϵ�ij��ʢˮͲ![]() �ӵ�P0�˶�����P����Ͳ���Ĺ���ԭ����֪�����ʢˮͲ����ˮ��ĸ߶�H(��λ:
�ӵ�P0�˶�����P����Ͳ���Ĺ���ԭ����֪�����ʢˮͲ����ˮ��ĸ߶�H(��λ: ![]() )������������������Ͳ��ת�ֵ�����O��ˮ��ľ���h��Ͳ���İ뾶r��Ͳ��ת���Ľ��ٶ�������λ:
)������������������Ͳ��ת�ֵ�����O��ˮ��ľ���h��Ͳ���İ뾶r��Ͳ��ת���Ľ��ٶ�������λ: ![]() ����ʢˮͲ�ij�ʼλ��P0�Լ���������ʱ��t(��λ:
����ʢˮͲ�ij�ʼλ��P0�Լ���������ʱ��t(��λ:![]() )����֪r=3
)����֪r=3![]() ��h=2
��h=2![]() ��Ͳ��ÿ����ת��(����ʱ�뷽��)1.5Ȧ�� ��P0����ˮ��ĸ߶�Ϊ3.5
��Ͳ��ÿ����ת��(����ʱ�뷽��)1.5Ȧ�� ��P0����ˮ��ĸ߶�Ϊ3.5![]() ����ʢˮͲM�ӵ�P0��ʼ����ʱ�䣬��������Ҫ����_______
����ʢˮͲM�ӵ�P0��ʼ����ʱ�䣬��������Ҫ����_______![]() �Ϳɵ�����ߵ㣻������
�Ϳɵ�����ߵ㣻������![]() ����ˮ��ĸ߶�
����ˮ��ĸ߶�![]() ��ʾΪʱ��
��ʾΪʱ��![]() �ĺ�������˺�������ʽΪ_________��
�ĺ�������˺�������ʽΪ_________��



ͼ1 ͼ2 ͼ3
���𰸡�![]()
![]()
��������
���������������ʼλ��![]() ��
��![]() �Ǹ�����ļнǣ���
�Ǹ�����ļнǣ���![]() ��һ�ε�����ߵ�ʱ�������ת���Ļ��ȣ�����Ͳ��ÿ����ת���Ļ��ȣ������һ�ε�����ߵ��ʱ�䣬���ɵó���һ�գ�
��һ�ε�����ߵ�ʱ�������ת���Ļ��ȣ�����Ͳ��ÿ����ת���Ļ��ȣ������һ�ε�����ߵ��ʱ�䣬���ɵó���һ�գ�
�����Ǻ����Ķ���ó�����![]() �������꣬���������������
�������꣬���������������![]() ����ˮ��ĸ߶�
����ˮ��ĸ߶�![]() �����ɵó��ڶ���.
�����ɵó��ڶ���.
��Ϊ��P0����ˮ��ĸ߶�Ϊ3.5![]() ����ʼʱ
����ʼʱ![]() ��
��![]() �Ǹ�����ļн�Ϊ
�Ǹ�����ļн�Ϊ![]()
�������֪��Ͳ��ÿ����ת��(����ʱ�뷽��)![]() ����Ͳ��ÿ����ת��
����Ͳ��ÿ����ת��![]()
��![]() ��һ�ε�����ߵ�ʱ����ת���Ļ���Ϊ
��һ�ε�����ߵ�ʱ����ת���Ļ���Ϊ![]() ��������ʱ��Ϊ
��������ʱ��Ϊ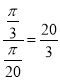
����ʢˮͲM�ӵ�P0��ʼ����ʱ�䣬��������Ҫ����![]()
![]() �Ϳɵ�����ߵ㣻
�Ϳɵ�����ߵ㣻
��![]() ��
��![]() �Ǹ�����ļн�Ϊ
�Ǹ�����ļн�Ϊ![]() ����
����![]()
�����Ǻ����Ķ����֪��![]() ��������Ϊ
��������Ϊ![]() ��
��![]()
���![]() ����ˮ��ĸ߶�
����ˮ��ĸ߶�![]() �ĺ���Ϊ
�ĺ���Ϊ![]() ��
��![]()
�ʴ�Ϊ��![]() ��
��![]()



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������![]() �У�����
�У�����![]() Ϊƽ���ı��Σ�
Ϊƽ���ı��Σ�![]() ����
����![]() ��
��![]() ����
����![]() ���е㣬��
���е㣬��![]() ��
��![]() ��
��

��1����֤��![]() ƽ��
ƽ��![]() ��
��
��2��������![]() �Ĵ�С��
�Ĵ�С��
��3�����![]() ����
����![]() ���е㣬��ֱ��
���е㣬��ֱ��![]() ��ƽ��
��ƽ��![]() ���ɽǵ�����ֵ��
���ɽǵ�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
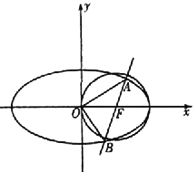
����Ŀ����֪������C�Ľ�����y���ϣ����㵽�ߵľ���Ϊ2���ҶԳ���Ϊy��.
��1����������C�ı����̣�
��2����������C�Ľ���Ϊ![]() ʱ����F��ֱ�߽��������ڣ�A��B���㣬��ֱ��OA��OB��OΪ����ԭ�㣩�ֱ�ֱ��
ʱ����F��ֱ�߽��������ڣ�A��B���㣬��ֱ��OA��OB��OΪ����ԭ�㣩�ֱ�ֱ��![]() ��M��N���㣬��
��M��N���㣬��![]() ����Сֵ.
����Сֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ԲG������������ԭ�㣬����һ������ΪԲF��x2+y2��2x��0��Բ�ģ��Ҷ�����ԲF��x���һ�����㣮��֪��ԲG��ֱ��l��x��my��1��0�ཻ��A��B���㣮
��I������Բ�ķ��̣�
�������AOB��������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪2017��![]() �о���ƽ����ͥ����������ͼ����ͥ������=��ͥ������һ��ͥ��֧��������ͼ��ʾ��������˵��������ǣ� ��
�о���ƽ����ͥ����������ͼ����ͥ������=��ͥ������һ��ͥ��֧��������ͼ��ʾ��������˵��������ǣ� ��

A. 2017��2�·�![]() �оӹ����ƽ����ͥ���������
�оӹ����ƽ����ͥ���������
B. 2017��4��5��6�·�![]() �о����ƽ����ͥ�������7��8��9�·ݵ�ƽ����ͥ�����벨��С
�о����ƽ����ͥ�������7��8��9�·ݵ�ƽ����ͥ�����벨��С
C. 2017����3����![]() �о����ƽ����ͥ���������4000Ԫ
�о����ƽ����ͥ���������4000Ԫ
D. 2017��9��10��11��12�·�ƽ����ͥ�������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�٣���ƽ���ı���![]() �У�
��![]() ��
��![]() ��
��![]() ��
��![]() �ڵ�
�ڵ�![]() ����
����![]() ��
��![]() ����ʹ
����ʹ![]() ������
������![]() ��
��![]() ���õ���ͼ����ʾ�ļ����壮
���õ���ͼ����ʾ�ļ����壮

��1����֤��ƽ��![]() ƽ��
ƽ��![]() ��
��
��2������![]() ���߶�
���߶�![]() �ϣ�ֱ��
�ϣ�ֱ��![]() ��ƽ��
��ƽ��![]() ���ɽǵ�����ֵΪ
���ɽǵ�����ֵΪ![]() ��������
��������![]() �������
�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��������������ϵ��
��������������ϵ��![]() ��
��![]() ��
��![]() ������ֻ��һ����ȷ������
������ֻ��һ����ȷ������![]() ��ֵ����__________��
��ֵ����__________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������![]() �Ľ���Ϊ
�Ľ���Ϊ![]() ������
������![]() ����ֱ��
����ֱ��![]() ���ֱ���������߽���
���ֱ���������߽���![]() ��
��![]() ���㣬�����߶�
���㣬�����߶�![]() Ϊֱ����Բ����
Ϊֱ����Բ����![]() .
.
(1)��������![]() �ķ��̣�
�ķ��̣�
(2)��ֱ��![]() ��������
��������![]() ����
����![]() ��
��![]() ���㣬��
���㣬��![]() Ϊ����
����![]() :
:![]() �ϵĶ��㣬��
�ϵĶ��㣬��![]() �������Сֵ.
�������Сֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���̵��ٻ�����֯6����Ա��������ǰϵ���������ǰ�ļ��ұ�������Ա���ڣ��μӶ��»�ѡ�����������õ�һ����Ϊ![]() �����ҵõڶ�����Ϊ
�����ҵõڶ�����Ϊ![]() �������õ�������Ϊ
�������õ�������Ϊ![]() ����
����![]() �������⣬
�������⣬![]() �Ǽ����⣬
�Ǽ����⣬![]() �������⣬��ѡ�����Ľ��Ϊ�� ��
�������⣬��ѡ�����Ľ��Ϊ�� ��
A.�õ�һ�����ҵõ����������õڶ���
B.��û�õ�һ������û�õڶ��������õ�����
C.�õ�һ������û�õڶ��������õ�����
D.�õڶ������ҵõ�һ�������õ�����
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com