
在透明塑料制成的正方体容器中灌进 体积的水,密封后可以任意摆放,那么容器内水面形状可能是:①三角形;②梯形;③长方形;④五边形.
体积的水,密封后可以任意摆放,那么容器内水面形状可能是:①三角形;②梯形;③长方形;④五边形.
其中正确的结果是 ( )
| A.①②③ | B.①③④ | C.②③④ | D.①②③④ |
D
解析试题分析:问题等价于用一个平面去截正方体,所截得的较小的几何体的体积为正方体体积的 ,假设正方体容器
,假设正方体容器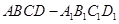 ,假设正方体
,假设正方体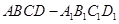 的棱长为
的棱长为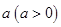 ,则正方体的体积
,则正方体的体积 ,
,
(1)当截面过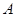 、
、 、
、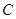 三点时,平面截正方体形成的较小的几何体为三棱锥
三点时,平面截正方体形成的较小的几何体为三棱锥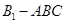 ,
,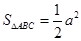 ,
,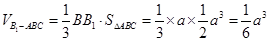 ,此时水面形状即截面图形形状为三角形;
,此时水面形状即截面图形形状为三角形;
(2)如下图所示,用不与棱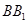 平行的平面截正方体
平行的平面截正方体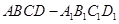 分别交
分别交 、
、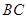 、
、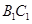 、
、 于
于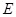 、
、 、
、 、
、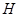 ,由于平面
,由于平面 平面
平面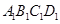 ,平面
,平面 平面
平面 ,平面
,平面 平面
平面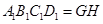 ,由平面与平面平行的性质定理知
,由平面与平面平行的性质定理知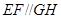 ,且
,且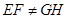 ,则截面图形
,则截面图形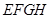 为梯形,则几何体
为梯形,则几何体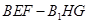 为台体,只需
为台体,只需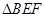 与
与 的面积满足一定的条件,能保证平面截正方体
的面积满足一定的条件,能保证平面截正方体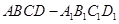 所形成的较小体积的几何体
所形成的较小体积的几何体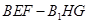 的体积为
的体积为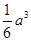 .
.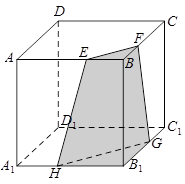
(3)如下图所示,用平行于棱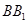 去截正方体
去截正方体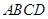 分别交
分别交 、
、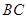 、
、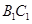 、
、 于
于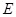 、
、 、
、 、
、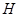 ,所形成的较小的几何体为三棱柱
,所形成的较小的几何体为三棱柱 ,当
,当 ,则三棱柱
,则三棱柱 的体积
的体积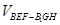
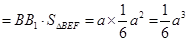 ,此时截面图形
,此时截面图形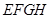 为矩形.
为矩形.
(4)如下图所示,在水面刚过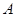 、
、 、
、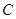 的时候,再将正方体容器
的时候,再将正方体容器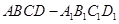 再倾斜一点,这时水面(即截面)分别交棱
再倾斜一点,这时水面(即截面)分别交棱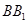 、
、 、
、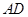 、
、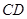 、
、 于点
于点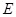 、
、 、
、 、
、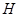 、
、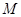 五点,将这五点连接起来便成为五边形
五点,将这五点连接起来便成为五边形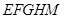 ,由平面与平面平行的性质定理知
,由平面与平面平行的性质定理知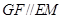 ,
, ,此时截面截正方体所形成的体积较小的几何体为多面体
,此时截面截正方体所形成的体积较小的几何体为多面体

 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:单选题
正方形AP1P2P3的边长为4,点B,C分别是边P1P2,P2P3的中点,沿AB,BC,CA折成一个三棱锥P-ABC(使P1,P2,P3重合于P),则三棱锥P-ABC的外接球表面积为 ( )
| A.24π | B.12π | C.8π | D.4π |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com