
【题目】已知圆C的方程:x2+y2﹣2x﹣4y+m=0,其中m<5.
(1)若圆C与直线l:x+2y﹣4=0相交于M,N两点,且|MN|= ![]() ,求m的值;
,求m的值;
(2)在(1)条件下,是否存在直线l:x﹣2y+c=0,使得圆上有四点到直线l的距离为 ![]() ,若存在,求出c的范围,若不存在,说明理由.
,若存在,求出c的范围,若不存在,说明理由.
【答案】
(1)解:圆的方程化为(x﹣1)2+(y﹣2)2=5﹣m,
圆心 C(1,2),半径 ![]() ,
,
则圆心C(1,2)到直线l:x+2y﹣4=0的距离为:
![]()
由于 ![]() ,则
,则 ![]() ,
,
有 ![]() ,
,
∴ ![]() ,解得m=4
,解得m=4
(2)解:假设存在直线l:x﹣2y+c=0,
使得圆上有四点到直线l的距离为 ![]() ,
,
由于圆心 C(1,2),半径r=1,
则圆心C(1,2)到直线l:x﹣2y+c=0的距离为:
![]() ,
,
解得 ![]()
【解析】(1)圆的方程化为(x﹣1)2+(y﹣2)2=5﹣m,圆心C(1,2)到直线l:x+2y﹣4=0的距离为 ![]() ,由此解得m=4.(2)假设存在直线l:x﹣2y+c=0,使得圆上有四点到直线l的距离为
,由此解得m=4.(2)假设存在直线l:x﹣2y+c=0,使得圆上有四点到直线l的距离为 ![]() ,由于圆心 C(1,2),半径r=1,由此利用圆心C(1,2)到直线l:x﹣2y+c=0的距离,能求出c的范围.
,由于圆心 C(1,2),半径r=1,由此利用圆心C(1,2)到直线l:x﹣2y+c=0的距离,能求出c的范围.


科目:高中数学 来源: 题型:
【题目】某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费![]() (单位:千元)对年销售量
(单位:千元)对年销售量![]() (单位:
(单位: ![]() )和年利润
)和年利润![]() (单位:千元)的影响.对近8年的年宣传费
(单位:千元)的影响.对近8年的年宣传费![]() 和年销售量
和年销售量![]() 数据作了初步处理,得到下面的散点图及一些统计量的值.
数据作了初步处理,得到下面的散点图及一些统计量的值.

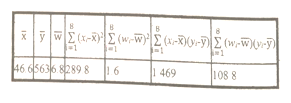
表中![]() .
.
(1)根据散点图判断![]() 与
与![]() 哪一个适宜作为年销售量
哪一个适宜作为年销售量![]() 关于年宣传费
关于年宣传费![]() 的回归类型?(给出判断即可,不必说明理由)
的回归类型?(给出判断即可,不必说明理由)
(2)根据(1)的判断结果及表中数据,建立![]() 关于
关于![]() 的回归方程;
的回归方程;
(3)已知这种产品的利润![]() 与
与![]() 的的关系为
的的关系为![]() .根据(2)的结果回答下列问题:
.根据(2)的结果回答下列问题:
(ⅰ)年宣传费![]() 时,年销售量及年利润的预报值是多少?
时,年销售量及年利润的预报值是多少?
(ⅱ)年宣传费![]() 为何值时,年利润的预报值最大?
为何值时,年利润的预报值最大?
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的的斜率和截距的最小二乘估计为
的的斜率和截距的最小二乘估计为 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,有一块半径长为1米的半圆形钢板,现要从中截取一个内接等腰 梯形部件ABCD,设梯形部件ABCD的面积为![]() 平方米.
平方米.
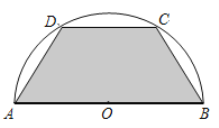
(1)按下列要求写出函数关系式:
①设![]() (米),将
(米),将![]() 表示成
表示成![]() 的函数关系式;
的函数关系式;
②设![]() ,将
,将![]() 表示成
表示成![]() 的函数关系式.
的函数关系式.
(2)求梯形部件ABCD面积![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}是首项为正数的等差数列,a1a2=3,a2a3=5.
(1)求数列{an}的通项公式;
(2)设bn=(an+1)2 ![]() ,求数列{bn}的前n项和Tn .
,求数列{bn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=4cosωxsin(ωx+ ![]() )+a(ω>0)图象上最高点的纵坐标为2,且图象上相邻两个最高点的距离为π. (Ⅰ)求a和ω的值;
)+a(ω>0)图象上最高点的纵坐标为2,且图象上相邻两个最高点的距离为π. (Ⅰ)求a和ω的值;
(Ⅱ)求函数f(x)在[0,π]上的单调递减区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=sin(ωx+φ)(ω>0,|φ|< ![]() )的图象如图所示,为了得到g(x)=sinωx的图象,则只要将f(x)的图象( )
)的图象如图所示,为了得到g(x)=sinωx的图象,则只要将f(x)的图象( ) 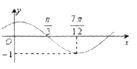
A.向左平移 ![]() 个单位长度
个单位长度
B.向右平移 ![]() 个单位长度
个单位长度
C.向右平移 ![]() 个单位长度
个单位长度
D.向左平移 ![]() 个单位长度
个单位长度
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图某综艺节目现场设有A,B,C,D四个观众席,现有由5不同颜色的马甲可供现场观众选择,同一观众席上的马甲的颜色相同,相邻观众席上的马甲的颜色不相同,则不同的安排方法种数为 . 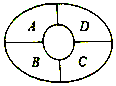
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com