
ΓΨΧβΡΩΓΩΈΣΩΦ≤λΗΏ÷–…ζΒΡ–‘±π”κ «Ζώœ≤ΜΕ ΐ―ßΩΈ≥Χ÷°ΦδΒΡΙΊœΒΘ§‘ΎΡ≥≥« –ΒΡΡ≥–ΘΗΏ÷–…ζ÷–Θ§¥”Ρ–…ζ÷–ΥφΜζ≥ι»ΓΝΥ70»ΥΘ§¥”≈°…ζ÷–ΥφΜζ≥ι»ΓΝΥ50»ΥΘ§Ρ–…ζ÷–œ≤ΜΕ ΐ―ßΩΈ≥ΧΒΡ’Φ![]() Θ§≈°…ζ÷–œ≤ΜΕ ΐ―ßΩΈ≥ΧΒΡ’Φ
Θ§≈°…ζ÷–œ≤ΜΕ ΐ―ßΩΈ≥ΧΒΡ’Φ![]() Θ§ΒΟΒΫ»γœ¬Ν–ΝΣ±μ.
Θ§ΒΟΒΫ»γœ¬Ν–ΝΣ±μ.
œ≤ΜΕ ΐ―ßΩΈ≥Χ | ≤Μœ≤ΜΕ ΐ―ßΩΈ≥Χ | ΚœΦΤ | |
Ρ–…ζ | |||
≈°…ζ | |||
ΚœΦΤ |
Θ®1Θ©«κΫΪΝ–ΝΣ±μ≤Ι≥δΆξ’ϊΘΜ ‘≈–ΕœΡήΖώ”–90%ΒΡΑ―Έ’»œΈΣœ≤ΜΕ ΐ―ßΩΈ≥Χ”κΖώ”κ–‘±π”–ΙΊΘΜ
Θ®2Θ©¥”≤Μœ≤ΜΕ ΐ―ßΩΈ≥ΧΒΡ―ß…ζ÷–≤…”ΟΖ÷≤ψ≥ι―υΒΡΖΫΖ®Θ§ΥφΜζ≥ι»Γ6»ΥΘ§œ÷¥”6»Υ÷–ΥφΜζ≥ι»Γ2»ΥΘ§«σ≥ι»ΓΒΡ―ß…ζ÷–÷Ν…Ό”–1Οϊ «≈°…ζΒΡΗ≈¬ ..
ΗΫΘΚ![]() Θ§Τδ÷–
Θ§Τδ÷–![]() .
.
| 0.150 | 0.100 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
ΓΨ¥πΑΗΓΩΘ®1Θ©ΦϊΫβΈωΘ§ΟΜ”–![]() ΒΡΑ―Έ’Θ®2Θ©
ΒΡΑ―Έ’Θ®2Θ©![]()
ΓΨΫβΈωΓΩ ‘ΧβΖ÷ΈωΘΚΘ®1Θ©ΫΪ ΐΨί¥ζ»κΩ®ΖΫΙΪ Ϋ«σΒΟ![]() Θ§‘ΌΕ‘’’≤ΈΩΦ ΐΨίΒΟΫα¬έΘ®2Θ©œ»ΗυΨίΖ÷≤ψ≥ι―υ»ΖΕ®≥ι»ΓΡ–…ζ≈°…ζ»Υ ΐΘ§‘Όάϊ”ΟΟΕΨΌΖ®»ΖΕ®¥”6»Υ÷–ΥφΜζ≥ι»Γ2»ΥΉή ¬Φΰ ΐΘ§¥”÷–»ΖΕ®÷Ν…Ό”–1Οϊ «≈°…ζ ¬Φΰ ΐΘ§ΉνΚσΗυΨίΙ≈ΒδΗ≈–ΆΗ≈¬ ΙΪ Ϋ«σΗ≈¬
Θ§‘ΌΕ‘’’≤ΈΩΦ ΐΨίΒΟΫα¬έΘ®2Θ©œ»ΗυΨίΖ÷≤ψ≥ι―υ»ΖΕ®≥ι»ΓΡ–…ζ≈°…ζ»Υ ΐΘ§‘Όάϊ”ΟΟΕΨΌΖ®»ΖΕ®¥”6»Υ÷–ΥφΜζ≥ι»Γ2»ΥΉή ¬Φΰ ΐΘ§¥”÷–»ΖΕ®÷Ν…Ό”–1Οϊ «≈°…ζ ¬Φΰ ΐΘ§ΉνΚσΗυΨίΙ≈ΒδΗ≈–ΆΗ≈¬ ΙΪ Ϋ«σΗ≈¬
‘ΧβΫβΈωΘΚΫβΘΚΘ®ΔώΘ©![]() Ν–ΝΣ±μ≤Ι≥δ»γœ¬ΘΚ
Ν–ΝΣ±μ≤Ι≥δ»γœ¬ΘΚ
œ≤ΜΕ ΐ―ßΩΈ≥Χ | ≤Μœ≤ΜΕ ΐ―ßΩΈ≥Χ | ΚœΦΤ | |
Ρ–…ζ |
|
|
|
≈°…ζ |
|
|
|
ΚœΦΤ |
|
|
|
”…Χβ“βΒΟ![]() Θ§
Θ§
ΓΏ![]() Θ§ΓύΟΜ”–
Θ§ΓύΟΜ”–![]() ΒΡΑ―Έ’»œΈΣœ≤ΜΕ ΐ―ßΩΈ≥Χ”κΖώ”κ–‘±π”–ΙΊΘ°Θ©
ΒΡΑ―Έ’»œΈΣœ≤ΜΕ ΐ―ßΩΈ≥Χ”κΖώ”κ–‘±π”–ΙΊΘ°Θ©
Θ®ΔρΘ©”ΟΖ÷≤ψ≥ι―υΒΡΖΫΖ®≥ι»Γ ±Θ§≥ι»Γ±»άΐ «![]() Θ§
Θ§
‘ρ≥ι»ΓΡ–…ζ![]() »ΥΘ§≥ι»Γ≈°…ζ
»ΥΘ§≥ι»Γ≈°…ζ![]() »ΥΘ°
»ΥΘ°
Φ«≥ι»ΓΒΡ≈°…ζΈΣ![]() Θ§≥ι»ΓΒΡΡ–…ζΈΣ
Θ§≥ι»ΓΒΡΡ–…ζΈΣ![]() Θ§
Θ§
¥”÷–ΥφΜζ≥ι»Γ![]() Οϊ―ß…ζΙ≤”–
Οϊ―ß…ζΙ≤”–![]() ÷÷«ιΩωΘΚ
÷÷«ιΩωΘΚ
![]()
![]() Θ°
Θ°
Τδ÷–÷Ν…Ό”–![]() Οϊ «≈°…ζΒΡ ¬ΦΰΈΣΘΚ
Οϊ «≈°…ζΒΡ ¬ΦΰΈΣΘΚ
![]() ”–
”–![]() ÷÷«ιΩωΘ°
÷÷«ιΩωΘ°
Φ«ΓΑ≥ι»ΓΒΡ―ß…ζ÷–÷Ν…Ό”–![]() Οϊ «≈°…ζΓ±ΈΣ ¬Φΰ
Οϊ «≈°…ζΓ±ΈΣ ¬Φΰ![]() Θ§‘ρ
Θ§‘ρ![]() Θ°
Θ°



| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΚ· ΐfΘ®xΘ©=sin ![]() +e©¹|x©¹1| Θ§ ”–œ¬Ν–ΥΡΗωΫα¬έΘΚ
+e©¹|x©¹1| Θ§ ”–œ¬Ν–ΥΡΗωΫα¬έΘΚ
ΔΌΆΦœσΙΊ”Ύ÷±œΏx=1Ε‘≥ΤΘΜ
ΔΎfΘ®xΘ©ΒΡΉν¥σ÷Β «2ΘΜ
ΔέfΘ®xΘ©ΒΡΉν¥σ÷Β «©¹1Θ§ΘΜ
ΔήfΘ®xΘ©‘Ύ«χΦδ[©¹2015Θ§2015]…œ”–2015ΗωΝψΒψΘ°
Τδ÷–’ΐ»ΖΒΡΫα¬έ «Θ®–¥≥ωΥυ”–’ΐ»ΖΒΡΫα¬έ–ρΚ≈Θ©Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘Ύ±Ώ≥ΛΈΣ4ΒΡΝβ–Έ![]() ÷–Θ§
÷–Θ§ ![]() Θ§Βψ
Θ§Βψ![]() ΓΔ
ΓΔ![]() Ζ÷±π‘Ύ±Ώ
Ζ÷±π‘Ύ±Ώ![]() ΓΔ
ΓΔ![]() …œΘ°Βψ
…œΘ°Βψ![]() ”κΒψ
”κΒψ![]() ΓΔ
ΓΔ![]() ≤Μ÷ΊΚœΘ§
≤Μ÷ΊΚœΘ§ ![]() Θ§
Θ§ ![]() Θ§―Ί
Θ§―Ί![]() ΫΪ
ΫΪ![]() Ζ≠’έΒΫ
Ζ≠’έΒΫ![]() ΒΡΈΜ÷ΟΘ§ ΙΤΫΟφ
ΒΡΈΜ÷ΟΘ§ ΙΤΫΟφ![]() ΤΫΟφ
ΤΫΟφ![]() Θ°
Θ°

Θ®ΔώΘ©«σ÷ΛΘΚ ![]() ΤΫΟφ
ΤΫΟφ![]() ΘΜ
ΘΜ
Θ®ΔρΘ©Φ«»ΐάβΉΕ![]() ΒΡΧεΜΐΈΣ
ΒΡΧεΜΐΈΣ![]() Θ§ΥΡάβΉΕ
Θ§ΥΡάβΉΕ![]() ΒΡΧεΜΐΈΣ
ΒΡΧεΜΐΈΣ![]() Θ§«“
Θ§«“![]() Θ§«σ¥Υ ±œΏΕΈ
Θ§«σ¥Υ ±œΏΕΈ![]() ΒΡ≥ΛΘ°
ΒΡ≥ΛΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΒψ![]() ΈΣ‘≤
ΈΣ‘≤![]() …œ“ΜΕ·ΒψΘ§
…œ“ΜΕ·ΒψΘ§![]() ÷α”ΎΒψ
÷α”ΎΒψ![]() Θ§»τΕ·Βψ
Θ§»τΕ·Βψ![]() ¬ζΉψ
¬ζΉψ![]() Θ®Τδ÷–
Θ®Τδ÷–![]() ΈΣΖ«Νψ≥Θ ΐΘ©
ΈΣΖ«Νψ≥Θ ΐΘ©
Θ®1Θ©«σΕ·Βψ![]() ΒΡΙλΦΘΖΫ≥ΧΘΜ
ΒΡΙλΦΘΖΫ≥ΧΘΜ
Θ®2Θ©Β±![]() ±Θ§ΒΟΒΫΕ·Βψ
±Θ§ΒΟΒΫΕ·Βψ![]() ΒΡΙλΦΘΈΣ«ζœΏ
ΒΡΙλΦΘΈΣ«ζœΏ![]() Θ§–±¬ ΈΣ
Θ§–±¬ ΈΣ![]() 1ΒΡ÷±œΏ
1ΒΡ÷±œΏ![]() ”κ«ζœΏ
”κ«ζœΏ![]() œύΫΜ”Ύ
œύΫΜ”Ύ![]() Θ§
Θ§![]() ΝΫΒψΘ§«σ
ΝΫΒψΘ§«σ![]() ΟφΜΐΒΡΉν¥σ÷Β.
ΟφΜΐΒΡΉν¥σ÷Β.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷Σ’ΐœν ΐΝ–{an}¬ζΉψa1=1Θ§Θ®n+1Θ©a2n+1+an+1an©¹na ![]() =0Θ§ ΐΝ–{bn}ΒΡ«ΑnœνΚΆΈΣSn«“Sn=1©¹bn Θ°
=0Θ§ ΐΝ–{bn}ΒΡ«ΑnœνΚΆΈΣSn«“Sn=1©¹bn Θ°
Θ®1Θ©«σ{an}ΚΆ{bn}ΒΡΆ®œνΘΜ
Θ®2Θ©Ννcn= ![]() Θ§ ΔΌ«σ{cn}ΒΡ«ΑnœνΚΆTnΘΜ
Θ§ ΔΌ«σ{cn}ΒΡ«ΑnœνΚΆTnΘΜ
ΔΎ «Ζώ¥φ‘Ύ’ΐ’ϊ ΐm¬ζΉψmΘΨ3Θ§c2 Θ§ c3 Θ§ cm≥…Β»≤ν ΐΝ–ΘΩ»τ¥φ‘ΎΘ§«κ«σ≥ωmΘΜ»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”…Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΚ· ΐfΘ®xΘ©=cosx+ax2©¹1Θ§aΓ RΘ°
Θ®1Θ©Β±a=0 ±Θ§«σΚ· ΐfΘ®xΘ©‘Ύ ![]() ¥ΠΒΡ«–œΏΖΫ≥ΧΘΜ
¥ΠΒΡ«–œΏΖΫ≥ΧΘΜ
Θ®2Θ©Β±a=1 ±Θ§«σΚ· ΐfΘ®xΘ©‘Ύ[©¹Π–Θ§Π–]…œΒΡΉν¥σ÷ΒΚΆΉν–Γ÷ΒΘΜ
Θ®3Θ©»τΕ‘”Ύ»Έ“βΒΡ Β ΐxΚψ”–fΘ®xΘ©Γί0Θ§«σ Β ΐaΒΡ»Γ÷ΒΖΕΈßΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΓςABCΒΡ»ΐΗωΡΎΫ«AΘ§BΘ§CΥυΕ‘ΒΡ±ΏΖ÷±πΈΣaΘ§bΘ§cΘ§œρΝΩ ![]() =Θ®c+aΘ§bΘ©Θ§
=Θ®c+aΘ§bΘ©Θ§ ![]() =Θ®c©¹aΘ§b©¹cΘ©Θ§«“
=Θ®c©¹aΘ§b©¹cΘ©Θ§«“ ![]() ΓΆ
ΓΆ ![]() Θ°
Θ°
Θ®1Θ©«σΫ«AΒΡ¥σ–ΓΘΜ
Θ®2Θ©»τa=3Θ§«σΓςABC÷ή≥ΛΒΡ»Γ÷ΒΖΕΈßΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣœρΝΩ ![]() ΚΆ
ΚΆ ![]() Θ§Τδ÷–
Θ§Τδ÷– ![]() Θ§
Θ§ ![]() Θ§kΓ RΘ°
Θ§kΓ RΘ°
Θ®1Θ©Β±kΈΣΚΈ÷Β ±Θ§”– ![]() ΓΈ
ΓΈ ![]() ΘΜ
ΘΜ
Θ®2Θ©»τœρΝΩ ![]() ”κ
”κ ![]() ΒΡΦ–Ϋ«ΈΣΕέΫ«Θ§«σ Β ΐkΒΡ»Γ÷ΒΖΕΈßΘ°
ΒΡΦ–Ϋ«ΈΣΕέΫ«Θ§«σ Β ΐkΒΡ»Γ÷ΒΖΕΈßΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§“―÷Σ’ΐΖΫ–ΈABCDΒΡ±Ώ≥ΛΈΣ6Θ§ΒψEΘ§FΖ÷±π‘Ύ±ΏABΘ§AD…œΘ§AE=AF=4Θ§œ÷ΫΪΓςAEF―ΊœΏΕΈEF’έΤπΒΫΓςAΓδEFΈΜ÷ΟΘ§ ΙΒΟAΓδC=2 ![]() Θ°
Θ° 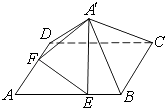
Θ®1Θ©«σΈεάβΉΕAΓδ©¹BCDFEΒΡΧεΜΐΘΜ
Θ®2Θ©«σΤΫΟφAΓδEF”κΤΫΟφAΓδBCΒΡΦ–Ϋ«Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com