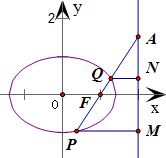
解:(Ⅰ)设点P的坐标为(x,y).
由题意知

•
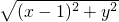
=|2-x|…(3分)
化简得x
2+2y
2=2,
∴动点P的轨迹方程为x
2+2y
2=2,即

+y
2=1--------(5分)
(Ⅱ)设直线FP的方程为x=ty+1,点P(x
1,y
1),Q(x
2,y
2)
因为△AQN∽△APM,所以PM=3QN,
由已知得PF=3QF,所以有y
1=-3y
2…(1)--------(7分)
由
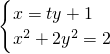
,消去x得(t
2+2)y
2+2ty-1=0,
∴△>0且y
1+y
2=-
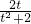
…(2),y
1y
2=-
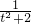
…(3)--------(10分)
联解(1)(2)(3),得t=-1,y
1=1,y
2=-

或t=1,y
1=-1,y
2=

∴存在点P(0,±1)使得△APM的面积是△AQN面积的9倍.--------(13分)
分析:(I)设点P的坐标为(x,y),根据点到直线的距离公式和两点间的距离公式,结合题意建立关于x、y的等式,化简整理可得x
2+2y
2=2,所以动点P的轨迹方程为椭圆

+y
2=1;
(II)设点P(x
1,y
1),Q(x
2,y
2).将直线FP方程x=ty+1与椭圆消去x,得到关于y的一元二次方程,结合根与系数的关系得到y
1+y
2和y
1y
2关于t的表达式.若△APM的面积是△AQN面积的9倍,由平几知识可得△AQN∽△APM,则PM=3QN,结合椭圆的性质得PF=3QF.因此得到y
1=-3y
2结合前面的等式,解出t=-1,从而得到存在点P(0,±1)使得△APM的面积是△AQN面积的9倍.
点评:本题给出动点P的轨迹是椭圆,探索椭圆的焦点弦所在直线与准线相交构成三角形的面积问题.着重考查了椭圆的简单几何性质、直线与椭圆的位置关系和三角形相似等知识,属于中档题.

 倍.
倍.
 •
•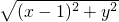 =|2-x|…(3分)
=|2-x|…(3分) +y2=1--------(5分)
+y2=1--------(5分)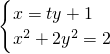 ,消去x得(t2+2)y2+2ty-1=0,
,消去x得(t2+2)y2+2ty-1=0,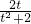 …(2),y1y2=-
…(2),y1y2=-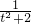 …(3)--------(10分)
…(3)--------(10分) 或t=1,y1=-1,y2=
或t=1,y1=-1,y2=
 +y2=1;
+y2=1;

 名校课堂系列答案
名校课堂系列答案 如图,正方体ABCD-A1B1C1D1的棱长为1,点M在AB上,且AM=
如图,正方体ABCD-A1B1C1D1的棱长为1,点M在AB上,且AM=