
【题目】苏州市一木地板厂生产A、B、C三类木地板,每类木地板均有环保型和普通两种型号,某月的产量如下表(单位:片):
类型 | 木地板A | 木地板B | 木地板C |
环保型 | 150 | 200 | Z |
普通型 | 250 | 400 | 600 |
按分层抽样的方法在这个月生产的木地板中抽取50片,其中A类木地板10片.
(1)求Z的值;
(2)用随机抽样的方法从B类环保木地板抽取8片,作为一个样本,经检测它们的得分如下:9.4、8.6、9.2、9.6、8.7、9.3、9.0、8.2,从中任取一个数,求该数与样本平均数之差的绝对不超过0.5的概率.
 精英口算卡系列答案
精英口算卡系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() .
.
(1)求f(x)+f(1﹣x)的值;
(2)若数列{an}满足an=f(0)+f( ![]() )+f(
)+f( ![]() )+…+f(
)+…+f( ![]() )+f(1)(n∈N*),求数列{an}的通项公式;
)+f(1)(n∈N*),求数列{an}的通项公式;
(3)若数列{bn}满足bn=2nan , Sn是数列{bn}的前n项和,是否存在正实数k,使不等式knSn>3bn对于一切的n∈N*恒成立?若存在,请求出k的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}中各项都大于1,前n项和为Sn , 且满足an2+3an=6Sn﹣2.
(1)求数列{an}的通项公式;
(2)令bn= ![]() ,求数列{bn}的前n项和Tn;
,求数列{bn}的前n项和Tn;
(3)求使得Tn< ![]() 对所有n∈N*都成立的最小正整数m.
对所有n∈N*都成立的最小正整数m.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】袋子A和B中装有若干个均匀的红球和白球,从A中摸出一个红球的概率是 ![]() ,从B中摸出一个红球的概率为p.
,从B中摸出一个红球的概率为p.
(1)从A中又放回的摸球,每次摸出一个,共摸5次 ①恰好有3次摸到红球的概率;
②第一次、第三次、第五次摸到红球的概率.
(2)若A、B两个袋子中的球之比为12,将A、B中的球装在一起后,从中摸出一个红球的概率是 ![]() ,求p的值.
,求p的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以直角坐标系的原点为极点O,![]() 轴正半轴为极轴,已知点P的直角坐标为(1,-5),点C的极坐标为
轴正半轴为极轴,已知点P的直角坐标为(1,-5),点C的极坐标为![]() ,若直线l经过点P,且倾斜角为
,若直线l经过点P,且倾斜角为![]() ,圆C的半径为4.
,圆C的半径为4.
(1).求直线l的参数方程及圆C的极坐标方程;
(2).试判断直线l与圆C有位置关系.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某省的一个气象站观测点在连续4天里记录的![]() 指数
指数![]() 与当天的空气水平可见度
与当天的空气水平可见度![]() (单位:
(单位: ![]() )的情况如表1:
)的情况如表1:

该省某市2016年11月![]() 指数频数分布如表2:
指数频数分布如表2:
|
|
|
|
|
|
频数 | 3 | 6 | 12 | 6 | 3 |
(1)设![]() ,根据表1的数据,求出
,根据表1的数据,求出![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(附参考公式: ![]() ,其中
,其中 ,
, ![]() )
)
(2)小李在该市开了一家洗车店,经统计,洗车店平均每天的收入与![]() 指数由相关关系,如表3:
指数由相关关系,如表3:
|
|
|
|
|
|
日均收入(元) |
|
|
|
|
|
根据表3估计小李的洗车店该月份平均每天的收入.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在对某渔业产品的质量调研中,从甲、乙两地出产的该产品中各随机抽取10件,测量该产品中某种元素的含量(单位:毫克).如图是测量数据的茎叶图: 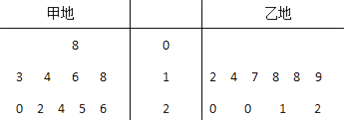
规定:当产品中的此种元素含量≥15毫克时为优质品.
(Ⅰ)试用上述样本数据估计甲、乙两地该产品的优质品率(优质品件数/总件数);
(Ⅱ)从乙地抽出的上述10件产品中,随机抽取3件,求抽到的3件产品中优质品数ξ的分布列及数学期望E(ξ).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com