
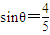 ,则
,则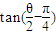 的值为( )
的值为( )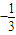

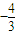
 的方程,求出方程的解得出tan
的方程,求出方程的解得出tan 的值,最后把所求式子利用两角和与差的正切函数公式及特殊角的三角函数值化简后,将tan
的值,最后把所求式子利用两角和与差的正切函数公式及特殊角的三角函数值化简后,将tan 的值代入即可求出值.
的值代入即可求出值.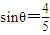 ,
,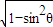 =-
=-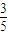 ,
, ,又tanθ=
,又tanθ=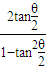 ,
,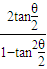 =-
=- ,即2tan2
,即2tan2 -3tan
-3tan -2=0,
-2=0, =-
=- (舍去),或tan
(舍去),或tan =2,
=2,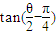 =
=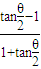 =
= .
.

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com