
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕ![]() жаЃЌЭждВ
жаЃЌЭждВ![]() ЃК
ЃК ![]() ЃЈ
ЃЈ![]() ЃЉЕФРыаФТЪЮЊ
ЃЉЕФРыаФТЪЮЊ![]() ЃЌСЌНгЭждВ
ЃЌСЌНгЭждВ![]() ЕФЫФИіЖЅЕуЫљаЮГЩЕФЫФБпаЮУцЛ§ЮЊ
ЕФЫФИіЖЅЕуЫљаЮГЩЕФЫФБпаЮУцЛ§ЮЊ![]() ЃЎ
ЃЎ

ЃЈ1ЃЉЧѓЭждВ![]() ЕФБъзМЗНГЬЃЛ
ЕФБъзМЗНГЬЃЛ
ЃЈ2ЃЉШєЭждВ![]() ЩЯЕу
ЩЯЕу![]() ЕНЖЈЕу
ЕНЖЈЕу![]() ЃЈ
ЃЈ![]() ЃЉЕФОрРыЕФзюаЁжЕЮЊ1ЃЌЧѓ
ЃЉЕФОрРыЕФзюаЁжЕЮЊ1ЃЌЧѓ![]() ЕФжЕМАЕу
ЕФжЕМАЕу![]() ЕФзјБъЃЛ
ЕФзјБъЃЛ
ЃЈ3ЃЉШчЭМЃЌЙ§ЭждВ![]() ЕФЯТЖЅЕузїСНЬѕЛЅЯрДЙжБЕФжБЯпЃЌЗжБ№НЛЭждВ
ЕФЯТЖЅЕузїСНЬѕЛЅЯрДЙжБЕФжБЯпЃЌЗжБ№НЛЭждВ![]() гкЕу
гкЕу![]() ЃЌ
ЃЌ ![]() ЃЌЩшжБЯп
ЃЌЩшжБЯп![]() ЕФаБТЪЮЊ
ЕФаБТЪЮЊ![]() ЃЌжБЯп
ЃЌжБЯп![]() ЃК
ЃК ![]() ЗжБ№гыжБЯп
ЗжБ№гыжБЯп![]() ЃЌ
ЃЌ ![]() НЛгкЕу
НЛгкЕу![]() ЃЌ
ЃЌ ![]() ЃЎМЧ
ЃЎМЧ![]() ЃЌ
ЃЌ ![]() ЕФУцЛ§ЗжБ№ЮЊ
ЕФУцЛ§ЗжБ№ЮЊ![]() ЃЌ
ЃЌ ![]() ЃЌЪЧЗёДцдкжБЯп
ЃЌЪЧЗёДцдкжБЯп![]() ЃЌЪЙЕУ
ЃЌЪЙЕУ![]() ЃПШєДцдкЃЌЧѓГіЫљгажБЯп
ЃПШєДцдкЃЌЧѓГіЫљгажБЯп![]() ЕФЗНГЬЃЛШєВЛДцдкЃЌЫЕУїРэгЩЃЎ
ЕФЗНГЬЃЛШєВЛДцдкЃЌЫЕУїРэгЩЃЎ
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЈ2ЃЉ
ЃЈ2ЃЉ![]() ЕФжЕЮЊ2ЃЌЕу
ЕФжЕЮЊ2ЃЌЕу![]() ЕФзјБъЮЊ
ЕФзјБъЮЊ![]() ЃЈ3ЃЉ
ЃЈ3ЃЉ![]() ЃЌ
ЃЌ ![]()
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉИљОнЬтвтСаГіЪНзг НтЕУ
НтЕУ ДгЖјЕУЕНЭждВЗНГЬЃЛЃЈ2ЃЉИљОнЕуЕуОрЙЋЪНЕУЕН
ДгЖјЕУЕНЭждВЗНГЬЃЛЃЈ2ЃЉИљОнЕуЕуОрЙЋЪНЕУЕН![]() ЃЌбаОПетИіКЏЪ§ЕФзюжЕМДПЩЃЛЃЈ3ЃЉСЊСЂжБЯпКЭЭждВЕУЕНЖўДЮЗНГЬЃЌ
ЃЌбаОПетИіКЏЪ§ЕФзюжЕМДПЩЃЛЃЈ3ЃЉСЊСЂжБЯпКЭЭждВЕУЕНЖўДЮЗНГЬЃЌ  ЃЌНЋУцЛ§БШзЊЛЏЮЊзјБъжЎБШДњШыМДПЩЁЃ
ЃЌНЋУцЛ§БШзЊЛЏЮЊзјБъжЎБШДњШыМДПЩЁЃ
НтЮіЃК
ЃЈ1ЃЉгЩЬтвтЕУЃК  НтЕУ
НтЕУ
ЫљвдЭждВ![]() ЕФБъзМЗНГЬЮЊ
ЕФБъзМЗНГЬЮЊ![]() ЃЎ
ЃЎ
ЃЈ2ЃЉЩш![]() ЃЌгЩЖЈЕу
ЃЌгЩЖЈЕу![]() ЃЌПМТЧОрРыЕФЦНЗНЃК
ЃЌПМТЧОрРыЕФЦНЗНЃК
дђ ЃЌ
ЃЌ
ЖўДЮКЏЪ§ЕФЭМЯѓЖдГЦжсЮЊ![]() ЃЌ
ЃЌ
гЩЭждВЗНГЬжЊ![]() ЃЌ
ЃЌ
гЩЬтЩшжЊ![]() ЃЌ
ЃЌ
ЂйЕБ![]() ЃЌМД
ЃЌМД![]() ЪБЃЌдк
ЪБЃЌдк![]() ЪБга
ЪБга![]() ЃЌ
ЃЌ
НтЕУ![]() ЃЌВЛЗћКЯЬтвтЃЌЩсШЅЃЛ
ЃЌВЛЗћКЯЬтвтЃЌЩсШЅЃЛ
ЂкЕБ![]() ЃЌМД
ЃЌМД![]() ЪБЃЌгЩЕЅЕїаджЊЃКдк
ЪБЃЌгЩЕЅЕїаджЊЃКдк![]() ЪБга
ЪБга![]() ЃЌ
ЃЌ
НтЕУ![]() Лђ
Лђ![]() ЃЈЩсЃЉЃЎ
ЃЈЩсЃЉЃЎ
злЩЯПЩЕУЃК ![]() ЕФжЕЮЊ2ЃЌЕу
ЕФжЕЮЊ2ЃЌЕу![]() ЕФзјБъЮЊ
ЕФзјБъЮЊ![]() ЃЎ
ЃЎ
ЃЈ3ЃЉгЩЃЈ1ЃЉжЊЃЌ ![]() ЃЌдђжБЯп
ЃЌдђжБЯп![]() ЕФЗНГЬЮЊ
ЕФЗНГЬЮЊ![]() ЃЌ
ЃЌ
СЊСЂ ЯћШЅ
ЯћШЅ![]() ВЂећРэЕУ
ВЂећРэЕУ![]() ЃЌНтЕУ
ЃЌНтЕУ![]() ЃЛ
ЃЛ
жБЯп![]() ЕФЗНГЬЮЊ
ЕФЗНГЬЮЊ![]() ЃЌЭЌРэПЩЕУ
ЃЌЭЌРэПЩЕУ![]() ЃЎ
ЃЎ
СЊСЂ НтЕУ
НтЕУ![]() ЃЌЭЌРэПЩЕУ
ЃЌЭЌРэПЩЕУ![]() ЃЌ
ЃЌ
Ыљвд ЃЌ
ЃЌ
МД![]() ЃЌНтЕУ
ЃЌНтЕУ![]() Лђ
Лђ![]() ЃЌ
ЃЌ
Ыљвд![]() Лђ
Лђ![]() ЃЌ
ЃЌ
ЙЪДцдкжБЯп![]() ЃК
ЃК ![]() ЃЌ
ЃЌ ![]() ТњзуЬтвтЃЎ
ТњзуЬтвтЃЎ


 дФЖСПьГЕЯЕСаД№АИ
дФЖСПьГЕЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЃЈБОЬтТњЗж8ЗжЃЉФГАр50УћбЇЩњдквЛДЮЪ§бЇВтЪджаЃЌГЩМЈШЋВПНщгк50гы100жЎМфЃЌНЋВтЪдНсЙћАДШчЯТЗНЪНЗжГЩЮхзщЃКЕквЛзщ[50ЃЌ60ЃЉЃЌЕкЖўзщ[60ЃЌ70ЃЉЃЌЁЃЌЕкЮхзщ[90ЃЌ100]ЃЎШчЭМЫљЪОЪЧАДЩЯЪіЗжзщЗНЗЈЕУЕНЕФЦЕТЪЗжВМжБЗНЭМЃЎ

ЃЈЂёЃЉШєГЩМЈДѓгкЛђЕШгк60ЧваЁгк80ЃЌШЯЮЊКЯИёЃЌЧѓИУАрдкетДЮЪ§бЇВтЪджаГЩМЈКЯИёЕФШЫЪ§ЃЛ
ЃЈЂђЃЉДгВтЪдГЩМЈдк[50ЃЌ60ЃЉЁШ[90ЃЌ100]ФкЕФЫљгабЇЩњжаЫцЛњГщШЁСНУћЭЌбЇЃЌЩшЦфВтЪдГЩМЈЗжБ№ЮЊmЁЂnЃЌЧѓЪТМўЁА|mЉn|ЃО10ЁБИХТЪЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЫФРтзЖPЉABCDЕФВрУцPADЪЧе§Ш§НЧаЮЃЌЕзУцABCDЮЊСтаЮЃЌAЕуEЮЊADЕФжаЕуЃЌШєBE=PEЃЎ 
ЃЈ1ЃЉЧѓжЄЃКPBЁЭBCЃЛ
ЃЈ2ЃЉШєЁЯPEB=120ЁуЃЌЧѓЖўУцНЧAЉPBЉCЕФгрЯвжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЩшЖЈвхдк![]() ЩЯЕФКЏЪ§
ЩЯЕФКЏЪ§![]() ЖдгкШЮвтЪЕЪ§
ЖдгкШЮвтЪЕЪ§![]() ЃЌЖМга
ЃЌЖМга![]() ГЩСЂЃЌЧв
ГЩСЂЃЌЧв![]() ЃЌЕБ
ЃЌЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЎ
ЃЎ
ЃЈ1ЃЉХаЖЯ![]() ЕФЕЅЕїадЃЌВЂМгвджЄУїЃЛ
ЕФЕЅЕїадЃЌВЂМгвджЄУїЃЛ
ЃЈ2ЃЉЪдЮЪЃКЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЪЧЗёгазюжЕ?ШчЙћгаЃЌЧѓГізюжЕЃЛШчЙћУЛгаЃЌЫЕУїРэгЩЃЛ
ЪЧЗёгазюжЕ?ШчЙћгаЃЌЧѓГізюжЕЃЛШчЙћУЛгаЃЌЫЕУїРэгЩЃЛ
ЃЈ3ЃЉНтЙигк![]() ЕФВЛЕШЪН
ЕФВЛЕШЪН![]() ЃЌЦфжа
ЃЌЦфжа![]() ЃЎ
ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§![]() дк
дк![]() ДІШЁЕУМЋаЁжЕ10ЃЌдђ
ДІШЁЕУМЋаЁжЕ10ЃЌдђ![]() ЕФжЕЮЊ__________ЃЎ
ЕФжЕЮЊ__________ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊвдЕуA(Ѓ1,2)ЮЊдВаФЕФдВгыжБЯпl1ЃКxЃЋ2yЃЋ7ЃН0ЯрЧаЃЎЙ§ЕуB(Ѓ2,0)ЕФЖЏжБЯпlгыдВAЯрНЛгкMЃЌNСНЕуЃЌQЪЧMNЕФжаЕуЃЎ
(1)ЧѓдВAЕФЗНГЬЃЛ
(2)ЕБ|MN|ЃН2![]() ЪБЃЌЧѓжБЯпlЕФЗНГЬЃЎ
ЪБЃЌЧѓжБЯпlЕФЗНГЬЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЃЈБОаЁЬтТњЗж10ЗжЃЉвбжЊКЏЪ§![]() ЪЧХМКЏЪ§ЃЎ
ЪЧХМКЏЪ§ЃЎ
ЃЈ1ЃЉЧѓЪЕЪ§![]() ЕФжЕ;
ЕФжЕ;
ЃЈ2ЃЉЩш![]() ,Шє
,Шє![]()
![]() гаЧвжЛгавЛИіЪЕЪ§Нт,ЧѓЪЕЪ§
гаЧвжЛгавЛИіЪЕЪ§Нт,ЧѓЪЕЪ§![]() ЕФШЁжЕЗЖЮЇЃЎ
ЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЖўДЮКЏЪ§f(x)Тњзуf(xЃЋ1)Ѓf(x)ЃНЃ2xЃЋ1ЃЌЧвf(2)ЃН15.
(1)ЧѓКЏЪ§f(x)ЕФНтЮіЪНЃЛ
(2) Сюg(x)ЃН(2Ѓ2m)xЃf(x)ЃЎ
Ђй ШєКЏЪ§g(x)дкxЁЪ[0ЃЌ2]ЩЯЪЧЕЅЕїКЏЪ§ЃЌЧѓЪЕЪ§mЕФШЁжЕЗЖЮЇЃЛ
Ђк ЧѓКЏЪ§g(x)дкxЁЪ[0ЃЌ2]ЩЯЕФзюаЁжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПНЋСНПщШ§НЧАхАДЭММзЗНЪНЦДКУЃЌЦфжа![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ
![]() ЃЌЯжНЋШ§НЧАх
ЃЌЯжНЋШ§НЧАх![]() би
би![]() елЦ№ЃЌЪЙ
елЦ№ЃЌЪЙ![]() дкЦНУц
дкЦНУц![]() ЩЯЕФЩфгА
ЩЯЕФЩфгА![]() ЧЁКУдк
ЧЁКУдк![]() ЩЯЃЌШчЭМввЃЎ
ЩЯЃЌШчЭМввЃЎ
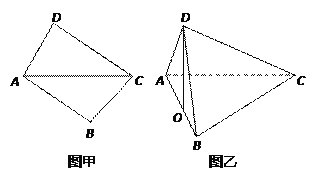
ЃЈ1ЃЉЧѓжЄЃК ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЧѓжЄЃК ![]() ЮЊЯпЖЮ
ЮЊЯпЖЮ![]() жаЕуЃЛ
жаЕуЃЛ
ЃЈ3ЃЉЧѓЖўУцНЧ![]() ЕФДѓаЁЕФе§ЯвжЕЃЎ
ЕФДѓаЁЕФе§ЯвжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com