Question

【题目】

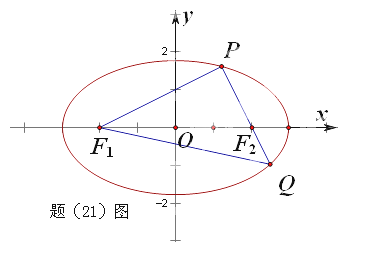
（2015·重庆）如题（21）图，椭圆的左右焦点分别为且过的直线交椭圆于两点，

且。

（1）若求椭圆的标准方程。
（2）若，且，试确定椭圆离心率的取值范围。

Answer 1

【答案】
（1）

（2）

【解析】（1）、由椭圆的定义，故.
设椭圆的半焦距为，由已知,因此,即.
最后由=1求得的值，从而根据椭圆的标准方程得到结果；
（2）、如图（21）图，由,得
由椭圆的定义，进而.
于是
解得故
由勾股定理得
从而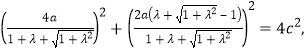
两边除以，得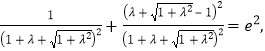
若记,则上式变成
由，并注意到关于的单调性，得即
进而即
【考点精析】根据题目的已知条件，利用函数的概念及其构成要素和椭圆的概念的相关知识可以得到问题的答案，需要掌握函数三要素是定义域，对应法则和值域，而定义域和对应法则是起决定作用的要素，因为这二者确定后，值域也就相应得到确定，因此只有定义域和对应法则二者完全相同的函数才是同一函数；平面内与两个定点，的距离之和等于常数（大于）的点的轨迹称为椭圆,这两个定点称为椭圆的焦点，两焦点的距离称为椭圆的焦距．