
【题目】已知动点![]() 到点
到点![]() 的距离与点
的距离与点![]() 到直线
到直线![]() 的距离的比值为
的距离的比值为![]() .
.
(1)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)设![]() 为轨迹
为轨迹![]() 与
与![]() 轴正半轴的交点,
轴正半轴的交点,![]() 上是否存在两点
上是否存在两点![]() ,使得
,使得![]() 是以
是以![]() 为直角顶点的等腰直角三角形?若存在,请说明满足条件的
为直角顶点的等腰直角三角形?若存在,请说明满足条件的![]() 的个数;若不存在,请说明理由.
的个数;若不存在,请说明理由.
【答案】(1)![]() (2)存在,3个
(2)存在,3个
【解析】
(1)设动点![]() 根据所给条件列出方程,化简即可.
根据所给条件列出方程,化简即可.
(2)由题意可知,直角边![]() 不可能垂直或平行于
不可能垂直或平行于![]() 轴,故可设
轴,故可设![]() 所在直线的方程为
所在直线的方程为![]() ,不妨设
,不妨设![]() ,则直线
,则直线![]() 所在的方程为
所在的方程为![]() . 联立直线与曲线方程,消元即可求出
. 联立直线与曲线方程,消元即可求出![]() 点的坐标,求出
点的坐标,求出![]() 的长,同理可得
的长,同理可得![]() ,再由
,再由![]() 得到方程,解得.
得到方程,解得.
解:(1)设动点![]() ,则
,则 ,
,
所以 ,
,
平方并化简,得![]() .
.
所以轨迹![]() 的方程为
的方程为![]() .
.
(2)存在. 理由如下:
由题意可知,直角边![]() 不可能垂直或平行于
不可能垂直或平行于![]() 轴,故可设
轴,故可设![]() 所在直线的方程为
所在直线的方程为![]() ,不妨设
,不妨设![]() ,则直线
,则直线![]() 所在的方程为
所在的方程为![]() .
.
联立方程![]() 消去
消去![]() ,并整理得
,并整理得![]() ,
,
解得![]() ,
,
将![]() 代入
代入![]() 可得
可得![]() ,
,
所以点![]() 的坐标为
的坐标为 .
.
所以 .
.
同理可得![]() ,
,
由![]() ,得
,得![]() ,
,
所以![]() ,则
,则![]() ,解得
,解得![]() 或
或![]() .
.
当![]() 斜率
斜率![]() 时,
时,![]() 斜率
斜率![]() ;当
;当![]() 斜率
斜率![]() 时,
时,![]() 斜率
斜率![]() ;当
;当![]() 斜率
斜率![]() 时,
时,![]() 斜率
斜率![]() .
.
综上所述,符合条件的三角形有3个.


 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案科目:高中数学 来源: 题型:
【题目】某地区经过一年的新农村建设,农村的经济收入增加了一倍.实现翻番.为更好地了解该地区农村的经济收入变化情况,统计了该地区新农村建设前后农村的经济收入构成比例.得到如下饼图:

则下面结论中不正确的是
A. 新农村建设后,种植收入减少
B. 新农村建设后,其他收入增加了一倍以上
C. 新农村建设后,养殖收入增加了一倍
D. 新农村建设后,养殖收入与第三产业收入的总和超过了经济收入的一半
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知椭圆![]()
![]() 的长轴
的长轴![]() ,长为4,过椭圆的右焦点
,长为4,过椭圆的右焦点![]() 作斜率为
作斜率为![]() (
(![]() )的直线交椭圆于
)的直线交椭圆于![]() 、
、![]() 两点,直线
两点,直线![]() ,
,![]() 的斜率之积为
的斜率之积为![]() .
.
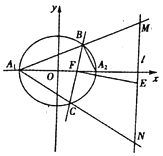
(1)求椭圆![]() 的方程;
的方程;
(2)已知直线![]() ,直线
,直线![]() ,
,![]() 分别与
分别与![]() 相交于
相交于![]() 、
、![]() 两点,设
两点,设![]() 为线段
为线段![]() 的中点,求证:
的中点,求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的右焦点为
的右焦点为![]() ,原点为
,原点为![]() ,椭圆
,椭圆![]() 的动弦
的动弦![]() 过焦点
过焦点![]() 且不垂直于坐标轴,弦
且不垂直于坐标轴,弦![]() 的中点为
的中点为![]() ,过
,过![]() 且垂直于线段
且垂直于线段![]() 的直线交射线
的直线交射线![]() 于点
于点![]() .
.
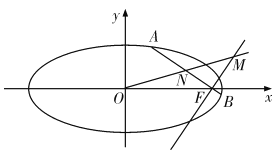
(Ⅰ)证明:点![]() 在定直线上;
在定直线上;
(Ⅱ)当![]() 最大时,求
最大时,求![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校学生会开展了一次关于“垃圾分类”问卷调查的实践活动,组织部分学生干部在几个大型小区随机抽取了共50名居民进行问卷调查.调查结束后,学生会对问卷结果进行了统计,并将其中一个问题“是否知道垃圾分类方法(知道或不知道)”的调查结果统计如下表:
年龄(岁) |
|
|
|
|
|
|
频数 |
|
| 14 | 12 | 8 | 6 |
知道的人数 | 3 | 4 | 8 | 7 | 3 | 2 |
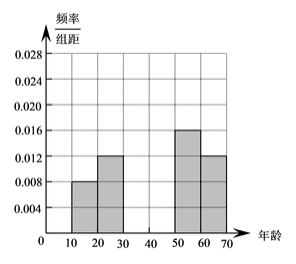
(1)求上表中的![]() 的值,并补全右图所示的的频率直方图;
的值,并补全右图所示的的频率直方图;
(2)在被调查的居民中,若从年龄在![]() 的居民中各随机选取1人参加垃圾分类知识讲座,求选中的两人中仅有一人不知道垃圾分类方法的概率
的居民中各随机选取1人参加垃圾分类知识讲座,求选中的两人中仅有一人不知道垃圾分类方法的概率
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若数列{an}满足:![]() ,且a1=1,则称{an}为一个X数列.对于一个X数列{an},若数列{bn}满足:b1=1,且
,且a1=1,则称{an}为一个X数列.对于一个X数列{an},若数列{bn}满足:b1=1,且![]() ,
,![]() ,则称{bn}为{an}的伴随数列.
,则称{bn}为{an}的伴随数列.
(Ⅰ)若X数列{an}中a2=1,a3=0,a4=1,写出其伴随数列{bn}中b2,b3,b4的值;
(Ⅱ)若{an}为一个X数列,{bn}为{an}的伴随数列,证明:“{an}为常数列”是“{bn}为等比数列”的充要条件.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年春节期间,我国高速公路继续执行“节假日高速公路免费政策”某路桥公司为掌握春节期间车辆出行的高峰情况,在某高速公路收费点记录了大年初三上午9:20~10:40这一时间段内通过的车辆数,统计发现这一时间段内共有600辆车通过该收费点,它们通过该收费点的时刻的频率分布直方图如下图所示,其中时间段9:20~9:40记作区间![]() ,9:40~10:00记作
,9:40~10:00记作![]() ,10:00~10:20记作
,10:00~10:20记作![]() ,10:20~10:40记作
,10:20~10:40记作![]() .例如:10点04分,记作时刻64.
.例如:10点04分,记作时刻64.

(1)估计这600辆车在9:20~10:40时间段内通过该收费点的时刻的平均值(同一组中的数据用该组区间的中点值代表);
(2)为了对数据进行分析,现采用分层抽样的方法从这600辆车中抽取10辆,再从这10辆车中随机抽取4辆,设抽到的4辆车中,在9:20~10:00之间通过的车辆数为X,求X的分布列与数学期望;
(3)由大数据分析可知,车辆在每天通过该收费点的时刻T服从正态分布![]() ,其中
,其中![]() 可用这600辆车在9:20~10:40之间通过该收费点的时刻的平均值近似代替,
可用这600辆车在9:20~10:40之间通过该收费点的时刻的平均值近似代替,![]() 可用样本的方差近似代替(同一组中的数据用该组区间的中点值代表),已知大年初五全天共有1000辆车通过该收费点,估计在9:46~10:40之间通过的车辆数(结果保留到整数).
可用样本的方差近似代替(同一组中的数据用该组区间的中点值代表),已知大年初五全天共有1000辆车通过该收费点,估计在9:46~10:40之间通过的车辆数(结果保留到整数).
参考数据:若![]() ,则
,则![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com