
如图,在长方体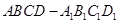 中,
中,
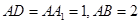 ,点
,点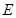 在棱
在棱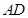 上移动
上移动

(Ⅰ)证明: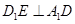 ;
;
(Ⅱ)当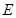 为
为 的中点时,求点
的中点时,求点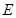 到面
到面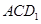 的距离;
的距离;
|
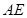 等于何值时,二面角
等于何值时,二面角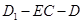 的大小为
的大小为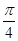
(Ⅰ)见解析(Ⅱ)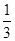 (Ⅲ)
(Ⅲ)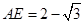
【解析】本小题主要考查向量语言表述线线的垂直、平行关系、点到平面的距离和线面关系等基本知识,同时考查空间想象能力和推理、运算能力.
(1)建立如图的坐标系,则
|
DA1 |
=(1,0,1),设E(1,t,0),则
|
D1E |
=(1,t,-1),通过向量的数量积为0,计算可得D1E⊥A1D;
(2)当E为AB的中点时,E(1,1,0),
|
D1E |
=(1,1,-1),求出平面ACD1的一个法向量,最后利用点到面的距离公式即可求点E到面ACD1的距离.
(3)(2)连接DE,根据等腰直角三角形的性质,及线面垂直的判定和性质,可得DE⊥EC,D1E⊥EC,进而由∠D1ED即为二面角D1-EC-D的平面角,解三角形D1ED即可得到二面角D1-EC-D的大小;
解:以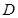 为坐标原点,直线
为坐标原点,直线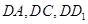 分别为
分别为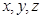 轴,建立空间直角坐标系,设
轴,建立空间直角坐标系,设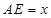 ,则
,则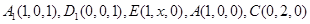
(Ⅰ)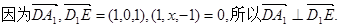 ………4分
………4分
(Ⅱ)因为 为
为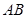 的中点,则
的中点,则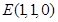 ,从而
,从而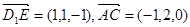 ,
,
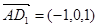 ,设平面
,设平面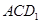 的法向量为
的法向量为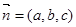 ,则
,则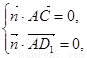
也即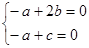 ,得
,得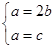 ,从而
,从而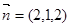 ,所以点
,所以点 到平面
到平面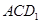 的距离为
的距离为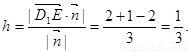 ………8分
………8分
(Ⅲ)设平面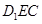 的法向量
的法向量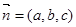 ,
,
∴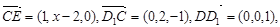
由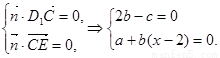 令
令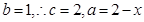 ,
,
∴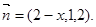
依题意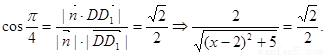
∴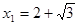 (不合,舍去),
(不合,舍去),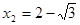
∴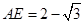 时,二面角
时,二面角 的大小为
的大小为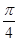 ………12分
………12分


 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案科目:高中数学 来源: 题型:
(08年惠州一中四模理) 如图,在长方体![]() 中,
中,![]() ,点E在棱
,点E在棱![]() 上移动。
上移动。
(Ⅰ)证明:![]() ;
;
(Ⅱ)当E为![]() 的中点时,求点E到面
的中点时,求点E到面![]() 的距离;
的距离;
(Ⅲ)![]() 等于何值时,二面角
等于何值时,二面角![]() 的大小为
的大小为![]() 。
。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com