
已知正方体的棱长为
a,分别求出它们的内切球、外接球及与各棱都相切的球的体积.|
正方体的内切球与各面的切点为正方体面的中心,故作出经过正方体相对面的中心且与棱平行的截面,则球的轴截面是其正方形截面的内切圆,如图所示,∴  . .
正方体的外接球与正方体的连接点为正方体各个顶点,故应作正方体对角面,则球的截面为其矩形截面的外接圆,如图,又矩形的两邻边分别为正方体两对角线和正方体的棱,则有 
∴外接球半径为 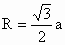 ,∴ ,∴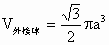 . .
与正方体的各棱均相切的球与正方体相连接的点是正方体各棱的中点,应作出经过正方体一组平行棱的中点的截面,则球的轴截面是其正方形截面的外接圆,如图,
求得球的半径为 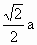
∴ 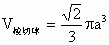 . .
|
|
这些都是几何体组合后产生的问题,为了准确求解,应分清它们是如何组合起来的,以转化为平面图形进行计算. (1) 相切或相接问题一般通过作出截面,使构成组合体的各个简单体中的主要元素尽可能集中在该截面上,从而化成平面图形的计算加以解决.(2) 旋转体之间的相接、相切问题,通常作出它们的共轴的截面;旋转体与多面体之间的相接、相切问题,一般作出它们“接”、“切”的某个公共点与轴所确定的截面. |


 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案科目:高中数学 来源:2012年人教B版高中数学必修2 2.4空间直角坐标系练习卷(解析版) 题型:解答题
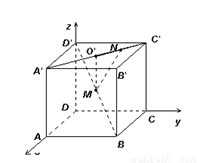
(14分)如图,已知正方体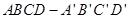 的棱长为a,M为
的棱长为a,M为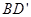 的中点,点N在
的中点,点N在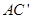 上,且
上,且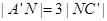 ,试求MN的长.
,试求MN的长.
查看答案和解析>>
科目:高中数学 来源:2012年人教A版高中数学选修2-1 3.1空间向量及其运算练习卷(解析版) 题型:解答题
(12分)如图,已知正方体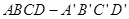 的棱长为a,M为
的棱长为a,M为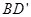 的中点,点N在
的中点,点N在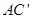 '上,且
'上,且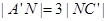 ,试求MN的长.
,试求MN的长.
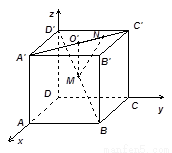
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com