练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】5名运动员参加一次乒乓球比赛，每名运动员都赛场并决出胜负．设第位运动员共胜场，负场（），则错误的结论是( )

    A.

    B.

    C. 为定值，与各场比赛的结果无关

    D. 为定值，与各场比赛结果无关

    【答案】D

    【解析】

    根据题意，对每个选项逐一分析即可得解。

    由题意得，所有胜的场数为10场，所以负的场数为10场。

    选项A，根据已知，所有胜的场数和与所有负的场数和是相等的，所以，即A选项正确。

    选项B，假设5名运动员胜的场数分别为0,1,2,3,4，则负的场数分别为4,3,2,1,0，所以，即选项B正确。

    选项C，=10，为定值，且与比赛结果无关，即选项C正确。

    选项D，不一定为定值，胜的场数可以0,1,2,3,4，也可以为1,1,1,3,4，故不一定为定值，所以选项D错误，故选D。

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】给出下列命题：

    ①命题“若，则”的否命题为“若，则”；

    ②“”是“”的必要不充分条件；

    ③命题“，使得”的否定是：“，均有”；

    ④命题“若，则”的逆否命题为真命题

    其中所有正确命题的序号是________.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】雾霾大气严重影响人们的生活，某科技公司拟投资开发新型节能环保产品，策划部制定投资计划时，不仅要考虑可能获得的盈利，而且还要考虑可能出现的亏损，经过市场调查，公司打算投资甲、乙两个项目，根据预测，甲、乙项目可能的最大盈利率分别为和，可能的最大亏损率分别为和，投资人计划投资金额不超过9万元，要求确保可能的资金亏损不超过万元．

    Ⅰ若投资人用x万元投资甲项目，y万元投资乙项目，试写出x，y所满足的条件，并在直角坐标系内作出表示x，y范围的图形．

    Ⅱ根据的规划，投资公司对甲、乙两个项目分别投资多少万元，才能使可能的盈利最大？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某学校运动会的立定跳远和30秒跳绳两个单项比赛分成预赛和决赛两个阶段.下表为10名学生的预赛成绩，其中有三个数据模糊.

    学生序号

    1

    2

    3

    4

    5

    6

    7

    8

    9

    10

    立定跳远（单位：米）

    1.96

    1.92

    1.82

    1.80

    1.78

    1.76

    1.74

    1.72

    1.68

    1.60

    30秒跳绳（单位：次）

    63

    a

    75

    60

    63

    72

    70

    a1

    b

    65

    在这10名学生中，进入立定跳远决赛的有8人，同时进入立定跳远决赛和30秒跳绳决赛的有6人，则

    （A）2号学生进入30秒跳绳决赛

    （B）5号学生进入30秒跳绳决赛

    （C）8号学生进入30秒跳绳决赛

    （D）9号学生进入30秒跳绳决赛

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】（本小题10分）选修4—4：坐标系与参数方程

    已知曲线C1的参数方程为（t为参数），以坐标原点为极点，x轴的正半轴为极轴建立极坐标系，曲线C2的极坐标方程为ρ=2sinθ。

    （Ⅰ）把C1的参数方程化为极坐标方程；

    （Ⅱ）求C1与C2交点的极坐标（ρ≥0,0≤θ＜2π）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在四棱锥中，底面是平行四边形，，侧面底面，,, 分别为的中点，点在线段上.

    （Ⅰ）求证：直线平面；

    （Ⅱ）若为的中点，求平面与平面所成锐二面角的余弦值；

    （Ⅲ）设，当为何值时，直线与平面所成角的正弦值为，求的值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，四棱锥的底面是正方形，每条侧棱的长都是底面边长的倍，为侧棱上的点.

    （1）求证：；

    （2）若平面，求二面角的大小；

    （3）在（2）的条件下，侧棱上是否存在一点，使得平面.若存在，求的值；若不存在，试说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】2018年10月28日，重庆公交车坠江事件震惊全国，也引发了广大群众的思考——如何做一个文明的乘客.全国各地大部分社区组织居民学习了文明乘车规范.社区委员会针对居民的学习结果进行了相关的问卷调查，并将得到的分数整理成如图所示的统计图.

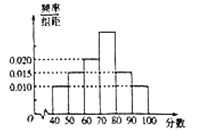
    （1）求得分在上的频率；

    （2）求社区居民问卷调查的平均得分的估计值；（同一组中的数据以这组数据所在区间中点的值作代表）

    （3）由于部分居民认为此项学习不具有必要性，社区委员会对社区居民的学习态度作调查，所得结果统计如下：（表中数据单位：人）

    认为此项学习十分必要

    认为此项学习不必要

    50岁以上

    400

    600

    50岁及50岁以下

    800

    200

    根据上述数据，计算是否有的把握认为居民的学习态度与年龄相关.

    附：，其中.

    0.100

    0.050

    0.010

    0.001

    2.706

    3.841

    6.635

    10.828

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在平面直角坐标系中，曲线的参数方程为 为参数），以原点为极点，以轴正半轴为极轴建立极坐标系，曲线的极坐标方程为，曲线，的公共点为.

    （Ⅰ）求直线的斜率；

    （Ⅱ）若点分别为曲线，上的动点，当取最大值时，求四边形的面积.

    查看答案和解析>>

    同步练习册答案