【题目】已知函数
， 
.
（1）求函数
的单调区间；
（2）若不等式
区间
上恒成立，求实数
的取值范围；
（3）求证： 
【答案】（1）函数
的单调递增区间为
，单调递减区间为
（2）
（3）见解析.
【解析】试题分析：（1）求出
，由
，结合函数的定义域解得
的范围，就是函数的增区间；（2）问题转化为
大于等于
的最大值，利用导数求得函数
有最大值，且最大值为
，得到
；（3）先判断
，得
，用放缩法证明
，即得要证的不等式.
试题解析：（1）∵
，故其定义域为
，
∴
，令
，得
，令
，得
.
故函数
的单调递增区间为
，单调递减区间为
.
（2）∵
， 
，∴
，令
又
，令
解得
.
当
在
内变化时， 
， 
变化如下表
|
|
|
|
| + | 0 | - |
|
由表知，当
时函数
有最大值，且最大值为
，所以， 
（3）由（2）知
，∴
（
）
∴
∴
即
【方法点晴】本题主要考查利用导数研究函数的单调性、证明不等式以及不等式恒成立问题，属于难题．不等式恒成立问题常见方法：① 分离参数
恒成立(
可)或
恒成立（
即可）；② 数形结合(
图象在
上方即可)；③ 讨论最值
或
恒成立；④ 讨论参数.本题（2）是利用方法 ① 求得
的最大值.
科目：高中数学 来源： 题型：
【题目】己知四棱锥
中， 
平面
，底面
是菱形，且
． 
， 
、
的中点分别为
， 
．
（Ⅰ）求证
．
（Ⅱ）求二面角
的余弦值．
（Ⅲ）在线段
上是否存在一点
，使得
平行于平面
？若存在，指出
在
上的位置并给予证明，若不存在，请说明理由．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】读下列各题所给的程序，依据程序画出程序框图，并说明其功能：
(1)INPUT “x＝”；x
IF x>1 OR x<－1 THEN
y＝1
ELSE y＝0
END IF
PRINE y
END
(2)INPUT “输入三个正数a，b，c＝”；a，b，c
IF a＋b>c AND a＋c>b AND b＋c>a THEN
p＝(a＋b＋c)/2
S＝SQR(p*(p－a)*(p－b)*(p－c))
PRINT “三角形的面积S＝”S
ELSE
PRINT “构不成三角形”
END IF
END
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，在海岛A上有一座海拔1千米的山，山顶设有一个观察站P，上午11时，测得一轮船在岛北偏东30°，俯角为30°的B处，到11时10分又测得该船在岛北偏西60°，俯角为60°的C处．
(1)求船的航行速度是每小时多少千米？
(2)又经过一段时间后，船到达海岛的正西方向的D处，问此时船距岛A有多远？
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知常数
，向量
， 
，经过点
，以
为方向向量的直线与经过点
，以
为方向向量的直线交于点
，其中
．
（
）求点
的轨迹方程，并指出轨迹
．
（
）若点
，当
时， 
为轨迹
上任意一点，求
的最小值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数
，其中
， 
．
（Ⅰ）当
时， 
的零点为______；（将结果直接填写在横线上）
（Ⅱ）当
时，如果存在
，使得
，试求
的取值范围；
（Ⅲ）如果对于任意
，都有
成立，试求
的最大值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知椭圆C的对称中心为原点O，焦点在x轴上，离心率为
，且点
在该椭圆上。
（I）求椭圆C的方程；
（II）过椭圆C的左焦点
的直线l与椭圆C相交于
两点，若
的面积为
，求圆心在原点O且与直线l相切的圆的方程。
查看答案和解析>>
科目：高中数学 来源： 题型：
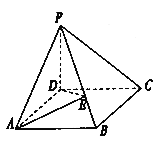
【题目】如图在棱锥
中， 
为矩形， 
面
， 
， 
与面
成
角， 
与面
成
角.
（1）在
上是否存在一点
，使
面
，若存在确定
点位置，若不存在，请说明理由；
（2）当
为
中点时，求二面角
的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
