Question

19. 如图，已知平行六面体ABCD－A₁B₁C₁D₁的底面ABCD是菱形，且∠C₁CB＝∠C₁CD＝∠BCD.

（Ⅰ）证明：C₁C⊥BD；

 

（Ⅱ）当的值为多少时，能使A₁C⊥平面C₁BD？请给出证明.

Answer 1

19.本小题主要考查直线与直线、直线与平面的关系，逻辑推理能力.

 

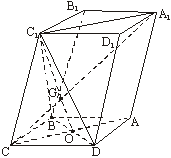
（Ⅰ）证明：连结A₁C₁、AC，AC和BD交于O，连结C₁O.

∵四边形ABCD是菱形，∴AC⊥BD，BC＝CD.

又∵∠BCC₁＝∠DCC₁，C₁C＝C₁C，∴△C₁BC≌△C₁DC，

∴C₁B＝C₁D.∵DO＝OB，∴C₁O⊥BD，       　

但　AC⊥BD，AC∩C₁O＝O，∴BD⊥平面AC₁.

又　C₁C平面AC₁，∴C₁C⊥BD.               　

 

（Ⅱ）当＝1时，能使A₁C⊥平面C₁BD.

 

证明一：∵＝1，∴BC＝CD＝C₁C，

 

又　∠BCD＝∠C₁CB＝∠C₁CD.

由此可推得　BD＝C₁B＝C₁D.

∴三棱锥C－C₁BD是正三棱锥.                    　

设　A₁C与C₁O相交于G.

∵A₁C₁∥AC，且A₁C₁∶OC＝2∶1，

∴C₁G∶GO＝2∶1.

又　C₁O是正三角形C₁BD的BD边上的高和中线，

∴点G是正三角形C₁BD的中心，∴CG⊥平面C₁BD.

即　A₁C⊥平面C₁BD.                        　

 

证明二：由（Ⅰ）知，BD⊥平面AC₁，

∵A₁C平面AC₁，

∴BD⊥A₁C.            　　　                

当＝1时，平行六面体的六个面是全等的菱形，

同BD⊥A₁C的证法可得BC₁⊥A₁C.

又　BD∩BC₁＝B，

∴A₁C⊥平面C₁BD.