
(满分12分)如图,正三棱柱ABC-A1B1C1的所有棱长都为2,D为CC1中点.

(1)求证:AB1⊥平面A1BD;
(2)求二面角A-A1D-B的余弦值;
(3)求点C1到平面A1BD的距离.
(1)见解析;(2) 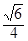 .(3)
.(3)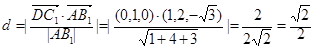 .
.
【解析】本题可以用空间向量法求解.第一步建系至关重要.取BC中点O,连结AO.∵△ABC为正三角形,∴AO⊥BC.∵在正三棱柱ABC-A1B1C1中,平面ABC⊥平面BCC1B1,∴AO⊥平面BCC1B1.取B1C1中点O1,以O为原点,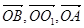 的方向为x,y,z轴的正方向建立空间直角坐标系.(1)根据向量垂直的坐标运算法则证明
的方向为x,y,z轴的正方向建立空间直角坐标系.(1)根据向量垂直的坐标运算法则证明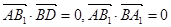 即可.
即可.
(2)设平面A1AD的法向量为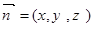 ,再根据
,再根据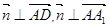 ,得到x,y,z之间的等式关系,进而得到一个满足条件的法向量,再根据
,得到x,y,z之间的等式关系,进而得到一个满足条件的法向量,再根据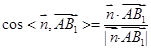 求解即可.
求解即可.
(3)利用向量求距离: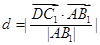 .
.
证明:(1)取BC中点O,连结AO.∵△ABC为正三角形,∴AO⊥BC.
∵在正三棱柱ABC-A1B1C1中,平面ABC⊥平面BCC1B1,∴AO⊥平面BCC1B1.
取B1C1中点O1,以O为原点,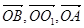 的方向为x,y,z轴的正方向建立空间直角坐标系,则B(1,0,0),D(-1,1,0),A1(0,2,
的方向为x,y,z轴的正方向建立空间直角坐标系,则B(1,0,0),D(-1,1,0),A1(0,2,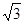 ),A(0,0,
),A(0,0,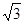 ),B1(1,2,0),
),B1(1,2,0),
∴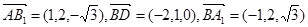 .
.
∴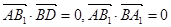
∴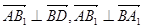 ,∴AB1
,∴AB1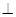 平面A1BD.
平面A1BD.
(2)设平面A1AD的法向量为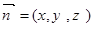 .
.
 =(-1,1,-
=(-1,1,-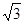 ),
),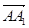 =(0,2,0).
=(0,2,0).
∵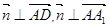 ,
,
∴
令z=1得n=(-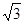 ,0,1)为平面A1AD的一个法向量.
,0,1)为平面A1AD的一个法向量.
由(1)知AB1⊥平面A1BD, 为平面A1BD的法向量.
为平面A1BD的法向量.
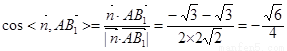 .
.
∴二面角A-A1D-B的大小的余弦值为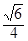 .
.
(3)C1点到A1BD的距离为
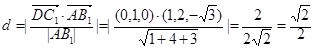 .
.


科目:高中数学 来源:2011年湖南省招生统一考试文科数学 题型:解答题
(本题满分12分)
如图3,在圆锥 中,已知
中,已知 的直径
的直径 的中点.
的中点.
(I)证明:
(II)求直线和平面 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年深圳市高三第一次调研考试数学文卷 题型:解答题
(本题满分12分)
如图,有一正方形钢板 缺损一角(图中的阴影部分),边缘线
缺损一角(图中的阴影部分),边缘线 是以直线AD为对称轴,以线段
是以直线AD为对称轴,以线段 的中点
的中点 为顶点的抛物线的一部分.工人师傅要将缺损一角切割下来,使剩余的部分成为一个直角梯形.若正方形的边长为2米,问如何画切割线
为顶点的抛物线的一部分.工人师傅要将缺损一角切割下来,使剩余的部分成为一个直角梯形.若正方形的边长为2米,问如何画切割线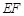 ,可使剩余的直角梯形的面积最大?并求其最大值.
,可使剩余的直角梯形的面积最大?并求其最大值.

查看答案和解析>>
科目:高中数学 来源:2010-2011学年深圳市高三第一次调研考试数学文卷 题型:解答题
(本小题满分12分)
如图,在四棱锥 中,
中, ,
, ,
, ,平面
,平面 平面
平面 ,
, 是线段
是线段 上一点,
上一点, ,
, ,
, .
.
(1)证明: 平面
平面 ;
;
(2)设三棱锥 与四棱锥
与四棱锥 的体积分别为
的体积分别为 与
与 ,求
,求 的值.
的值.

查看答案和解析>>
科目:高中数学 来源:岳阳市2010届高三第四次质检考试(数学文)试题 题型:解答题
(本小题满分12分)
如图,在三棱锥P-ABC中,AB⊥BC,AB=BC=PA=a,点O、D分别是AC、PC的中点,OP⊥底面ABC。

(1)求三棱锥P-ABC的体积;
(2)求异面直线PA与BD所成角余弦值的大小。
查看答案和解析>>
科目:高中数学 来源:2012届贵州省高二下学期期末考试理科数学 题型:解答题
(本小题满分12分)如图,在棱长为2的正方体 的中点,P为BB1的中点.
的中点,P为BB1的中点.
(I)求证 ;
;
(II)求异面直线 所成角的大小;
所成角的大小;

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com