
【题目】先后2次抛掷一次骰子,将得到的点数分别记为![]() .
.
(1)求直线![]() 与圆
与圆![]() 相切的概率;
相切的概率;
(2)将![]() ,4的值分别作为三条线段的长,求这三条线段能围成等腰三角形(含等边三角形)的概率.
,4的值分别作为三条线段的长,求这三条线段能围成等腰三角形(含等边三角形)的概率.
【答案】(1)![]() (2)
(2)![]() .
.
【解析】
本题考查的知识点是古典概型,我们要列出一枚骰子连掷两次先后出现的点数所有的情况个数
(1)再求出满足条件直线![]() 与圆
与圆![]() 相切的事件个数,然后代入古典概型公式即可求解;
相切的事件个数,然后代入古典概型公式即可求解;
(2)再求出满足条件![]() ,
,![]() ,4的值分别作为三条线段的长,求这三条线段能围成等腰三角形的事件个数,然后代入古典概型公式即可求解.
,4的值分别作为三条线段的长,求这三条线段能围成等腰三角形的事件个数,然后代入古典概型公式即可求解.
解:(1)总的事件的个数为:![]()
∵直线![]() 与圆
与圆![]() 相切
相切
![]() ,
,![]()
又![]()
∴满足条件的只有![]() 这种情况.
这种情况.
∴直线![]() 与圆
与圆![]() 相切的概率是
相切的概率是![]() .
.
(2)∵等腰三角形而边长为4
∴当![]() 时,
时,![]() ,即
,即![]() 共1种;
共1种;
当![]() 时,
时,![]() ,即
,即![]() 共1种;
共1种;
当![]() 时,
时,![]() ,即
,即![]() 共2种;
共2种;
当![]() 时,
时,![]() ,即
,即![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 共6种;
共6种;
当![]() 时,
时,![]() ,即
,即![]() 共2种;
共2种;
当![]() 时,
时,![]() ,即
,即![]() 共2种;
共2种;
∴满足条件的不同情况共有14种.
∴三条线段能围成不同的等腰三角形的概率为![]() .
.


科目:高中数学 来源: 题型:
【题目】如图,某小区中央广场由两部分组成,一部分是边长为![]() 的正方形
的正方形![]() ,另一部分是以
,另一部分是以![]() 为直径的半圆,其圆心为
为直径的半圆,其圆心为![]() .规划修建的
.规划修建的![]() 条直道
条直道![]() ,
, ![]() ,
, ![]() 将广场分割为
将广场分割为![]() 个区域:Ⅰ、Ⅲ、Ⅴ为绿化区域(图中阴影部分),Ⅱ、Ⅳ、Ⅵ为休闲区域,其中点
个区域:Ⅰ、Ⅲ、Ⅴ为绿化区域(图中阴影部分),Ⅱ、Ⅳ、Ⅵ为休闲区域,其中点![]() 在半圆弧上,
在半圆弧上, ![]() 分别与
分别与![]() ,
, ![]() 相交于点
相交于点![]() ,
, ![]() .(道路宽度忽略不计)
.(道路宽度忽略不计)
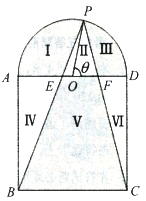
(1)若![]() 经过圆心,求点
经过圆心,求点![]() 到
到![]() 的距离;
的距离;
(2)设![]() ,
, ![]() .
.
①试用![]() 表示
表示![]() 的长度;
的长度;
②当![]() 为何值时,绿化区域面积之和最大.
为何值时,绿化区域面积之和最大.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学为了解高一学生的视力健康状况,在高一年级体检活动中采用统一的标准对数视力表,按照《中国学生体质健康监测工作手册》的方法对1039名学生进行了视力检测,判断标准为:双眼裸眼视力![]() 为视力正常,
为视力正常, ![]() 为视力低下,其中
为视力低下,其中![]() 为轻度,
为轻度, ![]() 为中度,
为中度, ![]() 为重度.统计检测结果后得到如图所示的柱状图.
为重度.统计检测结果后得到如图所示的柱状图.
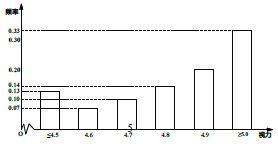
(1)求该校高一年级轻度近视患病率;
(2)根据保护视力的需要,需通知检查结果为“重度近视”学生的家长带孩子去医院眼科进一步检查和确诊,并开展相应的矫治,则该校高一年级需通知的家长人数约为多少人?
(3)若某班级6名学生中有2人为视力正常,则从这6名学生中任选2人,恰有1人视力正常的概率是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知抛物线![]() 的顶点在坐标原点,焦点在x轴上,且过点(2,4),圆
的顶点在坐标原点,焦点在x轴上,且过点(2,4),圆![]() ,过圆心
,过圆心![]() 的直线l与抛物线和圆分别交于P,Q,M,N,则
的直线l与抛物线和圆分别交于P,Q,M,N,则![]() 的最小值为________.
的最小值为________.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数据![]() 是宜昌市
是宜昌市![]() 个普通职工的年收入,设这
个普通职工的年收入,设这![]() 个数据的中位数为
个数据的中位数为![]() ,平均数为
,平均数为![]() ,方差为
,方差为![]() ,如果再加上世界首富的年收入
,如果再加上世界首富的年收入![]() ,则这
,则这![]() 个数据中,下列说法正确的是( )
个数据中,下列说法正确的是( )
A. 年收入平均数可能不变,中位数可能不变,方差可能不变
B. 年收入平均数大大增大,中位数可能不变,方差变大
C. 年收入平均数大大增大,中位数可能不变,方差也不变
D. 年收入平均数大大增大,中位数一定变大,方差可能不变
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的个数是( )
①设某大学的女生体重![]() 与身高
与身高![]() 具有线性相关关系,根据一组样本数据
具有线性相关关系,根据一组样本数据![]() ,用最小二乘法建立的线性回归方程为
,用最小二乘法建立的线性回归方程为![]() ,则若该大学某女生身高增加
,则若该大学某女生身高增加![]() ,则其体重约增加
,则其体重约增加![]() ;
;
②关于![]() 的方程
的方程![]() 的两根可分别作为椭圆和双曲线的离心率;
的两根可分别作为椭圆和双曲线的离心率;
③过定圆![]() 上一定点
上一定点![]() 作圆的动弦
作圆的动弦![]() ,
,![]() 为原点,若
为原点,若![]() ,则动点
,则动点![]() 的轨迹为椭圆;
的轨迹为椭圆;
④已知![]() 是椭圆
是椭圆![]() 的左焦点,设动点
的左焦点,设动点![]() 在椭圆上,若直线
在椭圆上,若直线![]() 的斜率大于
的斜率大于![]() ,则直线
,则直线![]() (
(![]() 为原点)的斜率的取值范围是
为原点)的斜率的取值范围是![]() .
.
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com