Question

在三棱柱ABC—A′B′C′中，侧面CBB′C′⊥底面ABC,∠B′BC=60°,∠ACB=90°，且CB=CC′=CA.

(1)求证：平面AB′C⊥平面A′C′B；

(2)求异面直线A′B与AC′所成的角.

Answer 1

思路解析：本题第一问，要证明面面垂直，可以依据面面垂直的判定定理来考虑，先证明其中一个面内的一条直线垂直于另外一个平面，而要证明一条直线垂直于一个平面，可以去证明这条直线垂直于另外一个平面内的相交的两条直线，转而证明相关的向量相互垂直，从而达到目的；第二问，可以转而去求相关的向量所成的角.

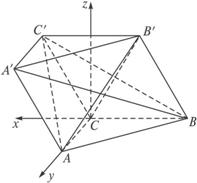
解：建立如图所示的空间直角坐标系.

设BC=2a,则A(0,2a,0)，B(-2a,0,0)，B′(-a,0,a)，C′(a,0,a)，A′(a,2a,a)，

则=(a,-2a,a)，=(-3a,-2a,-a)，=(-a,-2a,a)，=(3a,0,a)，=(-a,0,a).

(1)∵·=0，·=0,

∴BC′⊥CB′,BC′⊥AB′.

∴BC′⊥平面AB′C.

又BC′平面A′C′B，

∴平面AB′C⊥平面A′C′B.

(2)∵·=-2a²，||=4a，||=2a，

∴cos〈,〉=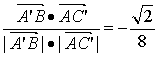.∴异面直线A′B与AC′所成的角为arccos.