分析:(1)对于直线l
1方程为x+y-3=0,令y=0,解得x,即可得到A.联立
,解得B.设C(0,y)(y<0),利用两点间的距离公式及
|AC|=2,解得y即可.
(2)利用点斜式可得直线AC的方程,再利用点到直线的距离公式可得点B到直线AC的距离d,即可得到
S△ABC=|AC|•d(3)设△ABC外接圆方程为x
2+y
2+Dx+Ey+F=0,把A(3,0),B(1,2),C(0,-
)代入得解出即可.
解答:解:(1)对于直线l
1方程为x+y-3=0,令y=0,解得x=3,∴A(3,0).
联立
,解得
,∴B(1,2).
设C(0,y)(y<0),∵
|AC|=2,∴
=2,解得y=-
,∴C
(0,-).
(2)直线AC的方程为
y=x-
,化为
x-y-1=0,
点B到直线AC的距离d=
=
,
∴
S△ABC=|AC|•d=
×2×=3.
(3)设△ABC外接圆方程为x
2+y
2+Dx+Ey+F=0,把A(3,0),B(1,2),C(0,-
)代入得
| | 9+3D=0 | | 1+22+D+2E+F=0 | | 3-E+F=0 |
| |
,解得D=-3,
E=2-,F=
2-6.
∴△ABC外接圆方程为
x2+y2-3x+(2-)y+2-6=0.
点评:熟练掌握直线的交点与方程联立的关系、点到直线的距离公式、三角形的面积计算公式、三角形外接圆的一般式方程等是解题的关键.



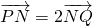 ,求直线L的方程.
,求直线L的方程.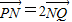 ,求直线L的方程.
,求直线L的方程.