
【题目】在平面直角坐标系xoy中,圆O的参数方程为![]() (
(![]() 为参数).过点(
为参数).过点(![]() )且倾斜角为
)且倾斜角为![]() 的直线
的直线![]() 与圆O交于A、B两点.
与圆O交于A、B两点.
(1)求![]() 的取值范围;
的取值范围;
(2)求AB中点P的轨迹的参数方程.
【答案】(1)![]() (2)
(2)
【解析】
(1)⊙O的普通方程为x2+y2=1,圆心为O(0,0),半径r=1,当α=![]() 时,直线l的方程为x=0,成立;当α≠
时,直线l的方程为x=0,成立;当α≠![]() 时,过点(0,﹣
时,过点(0,﹣![]() )且倾斜角为α的直线l的方程为y=tanαx+
)且倾斜角为α的直线l的方程为y=tanαx+![]() ,从而圆心O(0,0)到直线l的距离d=
,从而圆心O(0,0)到直线l的距离d=![]() <1,进而求出
<1,进而求出![]() 或
或![]() ,由此能求出α的取值范围.
,由此能求出α的取值范围.
(2)设直线l的方程为x=m(y+![]() ),联立
),联立![]() ,得(m2+1)y2+2
,得(m2+1)y2+2![]() +2m2﹣1=0,由此利用韦达定理、中点坐标公式能求出AB中点P的轨迹的参数方程.
+2m2﹣1=0,由此利用韦达定理、中点坐标公式能求出AB中点P的轨迹的参数方程.
(1)圆O的直角坐标方程为:![]() ,当
,当![]() 时,
时,![]() 与圆O交于两点,
与圆O交于两点,
当![]() 时,设
时,设![]() ,则
,则![]() 的方程为:
的方程为:![]()
![]() 与圆O交于两点当且仅当
与圆O交于两点当且仅当![]()
解得:![]() 或
或![]() ,即
,即![]() 或
或![]() ,
,
![]() .
.
(2) ![]() 的参数方程为:
的参数方程为:![]()
![]() ,
,
![]() ,
,
![]()
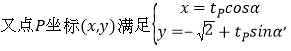 ,
,
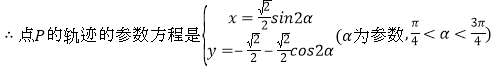 .
.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知集合M={(x,y)|f(x,y)=0},若对任意P1(x1 , y1)∈M,均不存在P2(x2 , y2)∈M使得x1x2+y1y2=0成立,则称集合M为“好集合”,下列集合为“好集合”的是( )
A.M={(x,y)|y﹣lnx=0}
B.M={(x,y)|y﹣![]() x2﹣1=0}
x2﹣1=0}
C.M={(x,y)|(x﹣2)2+y2﹣2=0}
D.M={(x,y)|x2﹣2y2﹣1=0}
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂有容量300吨的水塔一个,每天从早六点到晚十点供应生活和生产用水,已知:该厂生活用水每小时10吨,工业用水总量W(吨)与时间t(单位:小时,规定早晨六点时t=0)的函数关系为W=100 ![]() ,水塔的进水量有10级,第一级每小时水10吨,以后每提高一级,进水量增加10吨.若某天水塔原有水100吨,在供应同时打开进水管.问该天进水量应选择几级,既能保证该厂用水(即水塔中水不空),又不会使水溢出?
,水塔的进水量有10级,第一级每小时水10吨,以后每提高一级,进水量增加10吨.若某天水塔原有水100吨,在供应同时打开进水管.问该天进水量应选择几级,既能保证该厂用水(即水塔中水不空),又不会使水溢出?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() =1(a>b>0)的右焦点为F,过点F的直线交y轴于点N,交椭圆C于点A、P(P在第一象限),过点P作y轴的垂线交椭圆C于另外一点Q.若
=1(a>b>0)的右焦点为F,过点F的直线交y轴于点N,交椭圆C于点A、P(P在第一象限),过点P作y轴的垂线交椭圆C于另外一点Q.若 ![]() .
. 
(1)设直线PF、QF的斜率分别为k、k',求证: ![]() 为定值;
为定值;
(2)若 ![]() 且△APQ的面积为
且△APQ的面积为 ![]() ,求椭圆C的方程.
,求椭圆C的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知斜率为![]() 的直线
的直线![]() 与椭圆C:
与椭圆C:![]() 交于A、B两点,线段AB的中点为M(
交于A、B两点,线段AB的中点为M(![]() ),(m
),(m![]() )。
)。
(1)证明:![]() ;
;
(2)设F为C的右焦点,P为C上一点,且![]() +
+![]() +
+![]() =
=![]() ,证明:2|
,证明:2|![]() |=|
|=|![]() |+|
|+|![]() |.
|.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设正数x,y满足log ![]() x+log3y=m(m∈[﹣1,1]),若不等式3ax2﹣18xy+(2a+3)y2≥(x﹣y)2有解,则实数a的取值范围是( )
x+log3y=m(m∈[﹣1,1]),若不等式3ax2﹣18xy+(2a+3)y2≥(x﹣y)2有解,则实数a的取值范围是( )
A.(1, ![]() ]
]
B.(1, ![]() ]
]
C.[ ![]() ,+∞)
,+∞)
D.[ ![]() ,+∞)
,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ex+be﹣x﹣2asinx(a,b∈R).
(1)当a=0时,讨论函数f(x)的单调区间;
(2)当b=﹣1时,若f(x)>0对任意x∈(0,π)恒成立,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一台机器由于使用时间较长,生产的零件有一些缺损.按不同转速生产出来的零件有缺损的统计数据如下表所示:
转速x(转/秒) | 16 | 4 | 12 | 8 |
每小时生产有缺损零件数y(个) | 11 | 9 | 8 | 5 |
(1)作出散点图;
(2)如果y与x线性相关,求出回归直线方程;
(3)若实际生产中,允许每小时的产品中有缺损的零件最多为10个,那么,机器的运转速度应控制在什么范围内?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若a>0,b>0,则称 ![]() 为a,b的调和平均数.如图,点C为线段AB上的点,且AC=a,BC=b,点O为线段AB中点,以AB为直径做半圆,过点C作AB的垂线交半圆于D,连结OD,AD,BD.过点C作OD的垂线,垂足为E,则图中线段OD的长度是a,b的算术平均数,那么图中表示a,b的几何平均数与调和平均数的线段,以及由此得到的不等关系分别是( )
为a,b的调和平均数.如图,点C为线段AB上的点,且AC=a,BC=b,点O为线段AB中点,以AB为直径做半圆,过点C作AB的垂线交半圆于D,连结OD,AD,BD.过点C作OD的垂线,垂足为E,则图中线段OD的长度是a,b的算术平均数,那么图中表示a,b的几何平均数与调和平均数的线段,以及由此得到的不等关系分别是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com