
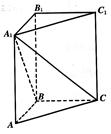
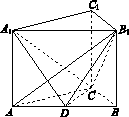
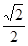 ,求点A到平面A1BC的距离.
,求点A到平面A1BC的距离.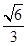 .
.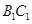 ∥
∥ ,就不需要另外作平行线了,还要注意的是异面直线所成的角不大于90°;(2)求点到平面的距离,一般要作出垂线段,求垂线段的长,即过点
,就不需要另外作平行线了,还要注意的是异面直线所成的角不大于90°;(2)求点到平面的距离,一般要作出垂线段,求垂线段的长,即过点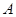 作平面
作平面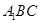 的垂线,首先观察寻找原有图形中的垂直关系,发现可证平面
的垂线,首先观察寻找原有图形中的垂直关系,发现可证平面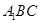 ⊥平面
⊥平面 ,因此我们只要在平面
,因此我们只要在平面 内作
内作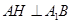 ,垂足为
,垂足为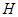 ,则可证
,则可证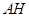 为所要求的垂线段,其长即为要求的距离.另外由于点
为所要求的垂线段,其长即为要求的距离.另外由于点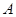 ,平面
,平面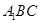 所在的三棱锥
所在的三棱锥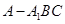 的体积很容易求得,故也可用体积法求解.
的体积很容易求得,故也可用体积法求解.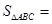
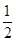 ,三棱柱
,三棱柱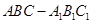 的体积
的体积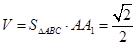 .
.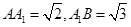 ,(2分)
,(2分) ⊥平面
⊥平面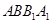 1,∴
1,∴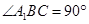 ,
,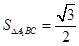 ,
,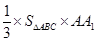 =三棱锥A-A1BC的体积V=
=三棱锥A-A1BC的体积V=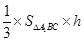 ,(6分)
,(6分)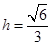 .(8分)
.(8分)

科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
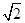 ,P是BC1上一动点,则CP+PA1的最小值是________.
,P是BC1上一动点,则CP+PA1的最小值是________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com