
【题目】在平面直角坐标系xOy中,已知曲线C1:![]() (t为参数),C2:
(t为参数),C2: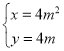 (m为参数).
(m为参数).
(1)将C1,C2的方程化为普通方程,并说明它们分别表示什么曲线;
(2)设曲线C1与C2的交点分别为A,B,O为坐标原点,求△OAB的面积的最小值.
【答案】(1)![]() sinθx-cosθy﹣2sin θ=0,
sinθx-cosθy﹣2sin θ=0,![]() y2=4x,(2)4
y2=4x,(2)4![]() .
.
【解析】
(1)C1:将![]() 两边同时乘以
两边同时乘以![]() 将
将![]() 两边同时乘以
两边同时乘以![]() ,消去参数t即可,C2消去m即可;
,消去参数t即可,C2消去m即可;
(2)联立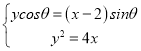 得y2sinθ﹣4ycosθ﹣8sinθ=0,设A(x1,y1),B(x2,y2),则y1+y2
得y2sinθ﹣4ycosθ﹣8sinθ=0,设A(x1,y1),B(x2,y2),则y1+y2![]() ,y1y2=﹣8,代入S△OAB=
,y1y2=﹣8,代入S△OAB=![]() |y1﹣y2|计算即可.
|y1﹣y2|计算即可.
(1)由C1:![]() (t为参数)消去t得C1:cosθy=sinθ(x﹣2),得sinθx-cosθy-2sinθ=0,
(t为参数)消去t得C1:cosθy=sinθ(x﹣2),得sinθx-cosθy-2sinθ=0,
由C2: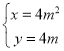 (m为参数)消去m得C2:y2=4x,
(m为参数)消去m得C2:y2=4x,
(2)联立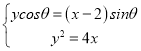 消去x得y2sinθ﹣4ycosθ﹣8sinθ=0,
消去x得y2sinθ﹣4ycosθ﹣8sinθ=0,
设A(x1,y1),B(x2,y2),则y1+y2![]() ,y1y2=﹣8,又C1与x轴的交点(2,0)
,y1y2=﹣8,又C1与x轴的交点(2,0)
∴S△OAB=![]() |y1﹣y2|
|y1﹣y2|![]()
![]()
=![]() ,
,
所以 sinθ=1时,SOAB取得最小值4![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】某企业拟生产一种如图所示的圆柱形易拉罐(上下底面及侧面的厚度不计),易拉罐的体积为![]() ,设圆柱的高度为
,设圆柱的高度为![]() ,底面半径为
,底面半径为![]() ,且
,且![]() ,假设该易拉罐的制造费用仅与其表面积有关.已知易拉罐侧面制造费用为
,假设该易拉罐的制造费用仅与其表面积有关.已知易拉罐侧面制造费用为![]() 元
元![]() ,易拉罐上下底面的制造费用均为
,易拉罐上下底面的制造费用均为![]() 元
元![]() 为常数).
为常数).
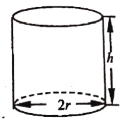
(1)写出易拉罐的制造费用![]() (元)关于
(元)关于![]() 的函数表达式,并求其定义域;
的函数表达式,并求其定义域;
(2)求易拉罐制造费用最低时![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() 为左右焦点,
为左右焦点,![]() 为短轴端点,长轴长为4,焦距为
为短轴端点,长轴长为4,焦距为![]() ,且
,且![]() ,
,![]() 的面积为
的面积为![]() .
.
(Ⅰ)求椭圆![]() 的方程
的方程
(Ⅱ)设动直线![]() 椭圆
椭圆![]() 有且仅有一个公共点
有且仅有一个公共点![]() ,且与直线
,且与直线![]() 相交于点
相交于点![]() .试探究:在坐标平面内是否存在定点
.试探究:在坐标平面内是否存在定点![]() ,使得以
,使得以![]() 为直径的圆恒过点
为直径的圆恒过点![]() ?若存在求出点
?若存在求出点![]() 的坐标,若不存在.请说明理由.
的坐标,若不存在.请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】用0与1两个数字随机填入如图所示的5个格子里,每个格子填一个数字,并且从左到右数,不管数到哪个格子,总是1的个数不少于0的个数,则这样填法的概率为__________.
![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,以坐标原点
中,以坐标原点![]() 务极点,
务极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() ,
,![]()
(1)求曲线![]() ,
,![]() 的直角坐标方程;
的直角坐标方程;
(2)曲线![]() 和
和![]() 的交点为
的交点为![]() ,
,![]() ,求以
,求以![]() 为直径的圆与
为直径的圆与![]() 轴的交点坐标.
轴的交点坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平行四边形![]() 中,
中,![]() ,
,![]() .现沿对角线
.现沿对角线![]() 将
将![]() 折起,使点
折起,使点![]() 到达点
到达点![]() .点
.点![]() 、
、![]() 分别在
分别在![]() 、
、![]() 上,且
上,且![]() 、
、![]() 、
、![]() 、
、![]() 四点共面.
四点共面.

(1)求证:![]() ;
;
(2)若平面![]() 平面
平面![]() ,平面
,平面![]() 与平面
与平面![]() 夹角为
夹角为![]() ,求
,求![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2x-1,![]() (a∈R),若对任意x1∈[1,+∞),总存在x2∈R,使f(x1)=g(x2),则实数a的取值范围是( )
(a∈R),若对任意x1∈[1,+∞),总存在x2∈R,使f(x1)=g(x2),则实数a的取值范围是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com