
(1)若![]() +
+![]() =0,求点M的坐标;
=0,求点M的坐标;
(2)求动点M的轨迹方程;
(3)求|![]() |的最小值.
|的最小值.
思路解析:(1)易求;(2)直接法,注意要“设而不求”;(3)二次函数区间上的最值问题,要注意讨论.
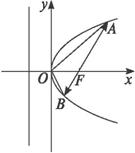
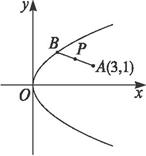
解:设A、B的坐标分别为(x1,y1)、(x2,y2),
则y12=2px1,y22=2px2.
(1)![]() =(x1-
=(x1-![]() ,y1),
,y1),![]() =(x2-
=(x2-![]() ,y2),
,y2),![]() +
+ ![]() =0,
=0,
∴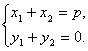 ∴2px1=2px2.∴x1=x2=
∴2px1=2px2.∴x1=x2=![]() .
.
∴![]() =(x,y)=
=(x,y)=![]() +
+![]() =(x1+x2,y1+y2)=(p,0).
=(x1+x2,y1+y2)=(p,0).
(2)![]() =(x,y)=(x1+x2,y1+y2),
=(x,y)=(x1+x2,y1+y2),
∴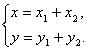 又
又![]() ∥
∥![]() ,∴y2(x1-
,∴y2(x1-![]() )=y1(x2-
)=y1(x2-![]() ).
).
∴y2(![]() -
-![]() )-y1(
)-y1(![]() -
-![]() )=0,
)=0,![]() (y1-y2)-
(y1-y2)-![]() (y2-y1)=0.
(y2-y1)=0.
∵y1≠y2,
∴y1y2=-p2,x=![]() (y12+y22)=
(y12+y22)=![]() [(y1+y2)2-2y1y2]=
[(y1+y2)2-2y1y2]=![]() [y2+2p2].
[y2+2p2].
∴y2=2px-2p2=2p(x-p).
∴动点M的轨迹方程为y2=2p(x-p).
(3)设M(x0,y0),由(2)知y02=2p(x0-p),
|![]() |2=x02+y02=x02+2px0-2p2=(x0+p)2-3p2,
|2=x02+y02=x02+2px0-2p2=(x0+p)2-3p2,
∵x0≥p,∴当x0=p时,|![]() |2有最小值p2,此时|
|2有最小值p2,此时|![]() |有最小值p.
|有最小值p.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
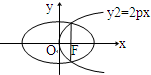
 如图所示,已知抛物线y2=2px(p>0)的焦点恰好是椭圆
如图所示,已知抛物线y2=2px(p>0)的焦点恰好是椭圆| x2 |
| a2 |
| y2 |
| b2 |
| 2 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图所示,已知抛物线C1:x2=y,圆M:x2+(y-4)2=1,点P是抛物线C1上一点(异于原点),过点P作圆M的两条切线,交抛物线C1于A,B两点,若过M,P两点的直线l垂直于AB,求直线l的方程.
如图所示,已知抛物线C1:x2=y,圆M:x2+(y-4)2=1,点P是抛物线C1上一点(异于原点),过点P作圆M的两条切线,交抛物线C1于A,B两点,若过M,P两点的直线l垂直于AB,求直线l的方程.查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
| x2 |
| a2 |
| y2 |
| b2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:2011-2012学年江苏省无锡市洛社高中高二(上)10月段考数学试卷(解析版) 题型:填空题
 的右焦点F,且两条曲线的交点连线也过焦点F,则该椭圆的离心率为 .
的右焦点F,且两条曲线的交点连线也过焦点F,则该椭圆的离心率为 .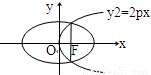
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com