
求下列函数的值域:
(1) y=x-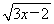 ;
;
(2) y=x2-2x-3,x∈(-1,4];
(3) y=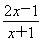 ,x∈[3,5];
,x∈[3,5];
(4) y=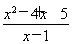 (x>1).
(x>1).
(1)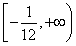 (2)[-4,5].(3)
(2)[-4,5].(3)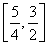 (4)[2
(4)[2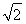 -2,+∞).
-2,+∞).
【解析】(1) (换元法)设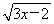 =t,t≥0,则y=
=t,t≥0,则y=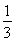 (t2+2)-t=
(t2+2)-t=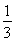
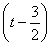 2-
2-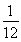 ,当t=
,当t=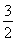 时,y有最小值-
时,y有最小值-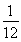 ,故所求函数的值域为
,故所求函数的值域为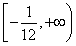 .
.
(2) (配方法)配方,得y=(x-1)2-4,因为x∈(-1,4],结合图象知,所求函数的值域为[-4,5].
(3) (解法1)由y=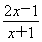 =2-
=2-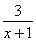 ,结合图象知,函数在[3,5]上是增函数,所以ymax=
,结合图象知,函数在[3,5]上是增函数,所以ymax=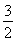 ,ymin=
,ymin=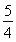 ,故所求函数的值域是
,故所求函数的值域是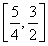 .
.
(解法2)由y=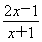 ,得x=
,得x=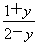 .因为x∈[3,5],所以3≤
.因为x∈[3,5],所以3≤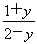 ≤5,解得
≤5,解得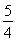 ≤y≤
≤y≤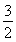 ,
,
即所求函数的值域是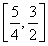 .
.
(4) (基本不等式法)令t=x-1,则x=t+1(t>0),
所以y=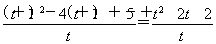 =t+
=t+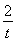 -2(t>0).
-2(t>0).
因为t+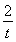 ≥2
≥2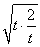 =2
=2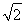 ,当且仅当t=
,当且仅当t=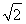 ,即x=
,即x=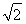 +1时,等号成立,
+1时,等号成立,
故所求函数的值域为[2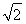 -2,+∞).
-2,+∞).


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第二章第6课时练习卷(解析版) 题型:解答题
已知二次函数f(x)满足f(2)=-1,f(-1)=-1,且f(x)的最大值为8,求二次函数f(x)的解析式.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第二章第4课时练习卷(解析版) 题型:填空题
函数f(x)=mx2+(2m-1)x+1是偶函数,则实数m=________.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第二章第3课时练习卷(解析版) 题型:填空题
函数y=f(x)是定义在[-2,2]上的单调减函数,且f(a+1)<f(2a),则实数a的取值范围是________.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第二章第2课时练习卷(解析版) 题型:填空题
下列四组函数中的f(x)与g(x)表示同一函数的有________.(填序号)
① f(x)=x0,g(x)=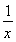 ;
;
② f(x)=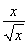 ,g(x)=
,g(x)=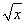 ;
;
③ f(x)=x2,g(x)=(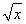 )4;
)4;
④ f(x)=|x|,g(x)=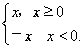
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第二章第14课时练习卷(解析版) 题型:填空题
在平面直角坐标系xOy中,设定点A(a,a),P是函数y=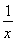 (x>0)图象上一动点.若点P、A之间的最短距离为2
(x>0)图象上一动点.若点P、A之间的最短距离为2 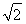 ,则满足条件的实数a的所有值为________.
,则满足条件的实数a的所有值为________.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第二章第12课时练习卷(解析版) 题型:填空题
若函数f(x)=x2+ax+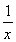 在
在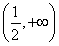 上是增函数,则a的取值范围是________.
上是增函数,则a的取值范围是________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com