
(Ⅰ)求该选手被淘汰的概率;
(Ⅱ)该选手在选拔中回答问题的个数记为ξ,求随机变量ξ的分布列与数学期望.
解法一: (Ⅰ)记“该选手能正确回答第i轮的问题”的事情为Ai(i=1,2,3),则P(A1)=![]() ,P(A2)=
,P(A2)=![]() , P(A3)=
, P(A3)=![]() ,∴该选手被淘汰的概率
,∴该选手被淘汰的概率
P=P(![]() +A1
+A1![]() +A1A2
+A1A2![]() )
)
=P(![]() )+P(A1)P(
)+P(A1)P(![]() )+P(A1)P(A2)P(
)+P(A1)P(A2)P(![]() )=
)=![]()
(Ⅱ)ξ的可能值为1,2,3.
P(ξ=1)=P(![]() )=
)=![]() ,
,
P(ξ=2)=P(A1![]() )=P(A1)P(
)=P(A1)P(![]() )=
)=![]()
P(ξ=3)=P(A1A2)=P(A1)P(A2)=![]()
∴ξ的分布列为
ξ | 1 | 2 | 3 |
P |
|
|
|
∴Eξ=1×![]() +2×
+2×![]() +3×
+3×![]() =
=![]()
解法二: (Ⅰ)记“该选手能正确回答第i轮的问题”的事件为Ai(i=1,2,3),则P(A1)=![]() , P(A2)=
, P(A2)=![]() , P(A3)=
, P(A3)=![]() . ∴该选手被淘汰的概率P=1-P(
. ∴该选手被淘汰的概率P=1-P(![]() )=1-P(
)=1-P(![]() )P(
)P(![]() )P(
)P(![]() )=1-
)=1-![]()
(Ⅱ)同解法一.


 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案 期末好成绩系列答案
期末好成绩系列答案科目:高中数学 来源: 题型:
| 4 |
| 5 |
| 3 |
| 5 |
| 2 |
| 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:
(08年龙岩一中模拟理)(12分)
某项选拔共有三轮考核,每轮设有一个问题,能正确回答问题者进入下一轮考试,否则即被淘汰,已知某选手能正确回答第一、二、三轮的问题的概率分别为![]() 、
、![]() 、
、![]() ,且各轮问题能否正确回答互不影响.
,且各轮问题能否正确回答互不影响.
(1)求该选手被淘汰的概率;
(2)该选手在选拔中回答问题的个数记为ξ,求随机变量ξ的分布列与数数期望.(注:本小题结果可用分数表示)
查看答案和解析>>
科目:高中数学 来源: 题型:
(08年海拉尔二中阶段考试五理) 某项选拔共有三轮考核,每轮设有一问题,能正确回答问题者进入下一轮考核,否则即被淘汰.已知某选手能正确回答第一、二、三、轮的问题的概率分别为![]() 且各轮问题能否正确回答互不影响.
且各轮问题能否正确回答互不影响.
(Ⅰ)求该选手被淘汰的概率;
(Ⅱ)该选手在选择中回答问题的个数记为![]() ,求随机变量
,求随机变量![]() 的分布列与数学期望.
的分布列与数学期望.
(注:本小题结果可用分数表示)
查看答案和解析>>
科目:高中数学 来源: 题型:
某项选拔共有三轮考核,每轮设有一个问题,能正确回答问题者进入下一轮考试,否则即被淘汰,已知某选手能正确回答第一、二、三轮的问题的概率分别为![]() 、
、![]() 、
、![]() ,且各轮问题能否正确回答互不影响.
,且各轮问题能否正确回答互不影响.
(Ⅰ)求该选手被淘汰的概率;
(Ⅱ)该选手在选拔中回答问题的个数记为ξ,求随机变量ξ的分布列与数数期望.(注:本小题结果可用分数表示)
查看答案和解析>>
科目:高中数学 来源:2012-2013学年重庆市高三3月月考理科数学试卷(解析版) 题型:解答题
某项选拔共有三轮考核,每轮设有一个问题,能正确回答问题者进入下一轮考试,否则即被淘汰,已知某选手能正确回答第一、二、三轮的问题的概率分别为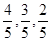 且各轮问题能否正确回答互不影响.
且各轮问题能否正确回答互不影响.
(Ⅰ)求该选手被淘汰的概率;
(Ⅱ)该选手在选拔中回答问题的个数记为ξ,求随机变量ξ的分布列与数学期望.
(注:本小题结果可用分数表示)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com