解:(1)已知的等式
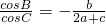
,
由正弦定理得:
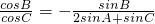
,(2分)
-sinBcosC=2cosBsinA+cosBsinC(3分)
sinBcosC+cosBsinC+2cosBsinA=0,
sin(B+C)+2cosBsinA=0,(4分)
sinA+2cosBsinA=0,(只要写出本行,给5分)(5分)
因为sinA≠0,
所以cosB=-

,所以B=120°;(7分)
(2)由余弦定理得:b
2=a
2+c
2-2accosB,(9分)
19=(a+c)
2-2ac-2accos120°,所以ac=6,(11分)
由
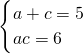
,
解得
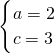
或
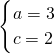
.(缺一解,扣1分)(14分)
分析:(1)利用正弦定理化简已知的等式,移项后再利用两角和与差的正弦函数公式及诱导公式化简,根据sinA不为0,得出cosB的值,由B为三角形的内角,利用特殊角的三角函数值即可求出B的度数;
(2)由第一问求出的B的度数,得出cosB的值,利用余弦定理表示出b
2,把b及cosB的值代入,配方后再把a+c的值代入可得出ac=6,与a+c=5联立成方程组,求出方程组的解即可求出a与c的值.
点评:此题考查了正弦、余弦定理,两角和与差的正弦函数公式,以及特殊角的三角函数值,熟练掌握定理及公式是解本题的关键.

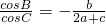 .
. ,a+c=5,求a和c的值.
,a+c=5,求a和c的值.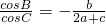 ,
,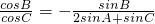 ,(2分)
,(2分) ,所以B=120°;(7分)
,所以B=120°;(7分)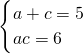 ,
,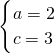 或
或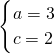 .(缺一解,扣1分)(14分)
.(缺一解,扣1分)(14分)
