
 (a,b>0),其右焦点F2(1,0),右准线为x=2,斜率为k的直线l过椭圆C的右焦点,并且和椭圆相交于M,N.
(a,b>0),其右焦点F2(1,0),右准线为x=2,斜率为k的直线l过椭圆C的右焦点,并且和椭圆相交于M,N. ,问点P能否落在椭圆C的外部,如果会,求出斜率k的取值范围;不会,说明理由;
,问点P能否落在椭圆C的外部,如果会,求出斜率k的取值范围;不会,说明理由; ,求λ的取值范围.
,求λ的取值范围. ,可得a,b的值,最后写出椭圆C的方程;
,可得a,b的值,最后写出椭圆C的方程; ,得出y1与y2的关系式,利用根与系数的关系得出k与λ的等式,由k>0,得出关于λ的不等关系,解得λ的取值范围.
,得出y1与y2的关系式,利用根与系数的关系得出k与λ的等式,由k>0,得出关于λ的不等关系,解得λ的取值范围. ,
, ;
; ,
, ,y1+y2=
,y1+y2= .
. ,
, ,
, .
. 时,点P在椭圆的外部
时,点P在椭圆的外部 ,
, ,
, ,
, ,
, ,
, ,且λ≠1.即为λ的取值范围.
,且λ≠1.即为λ的取值范围.

科目:高中数学 来源: 题型:解答题
 (a>0),其焦点在x轴上,点Q
(a>0),其焦点在x轴上,点Q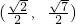 为椭圆上一点.
为椭圆上一点.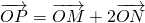 ,其中M、N是椭圆C上的点,直线OM与ON的斜率之积为
,其中M、N是椭圆C上的点,直线OM与ON的斜率之积为 ,求证:
,求证: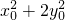 为定值;
为定值;查看答案和解析>>
科目:高中数学 来源: 题型:
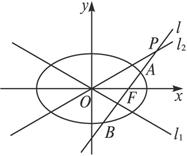
(1)当l1与l2夹角为60°,双曲线的焦距为4时,求椭圆C的方程;
(2)当![]() =λ
=λ![]() 时,求λ的最大值.
时,求λ的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
(1)当l1与l2夹角为60°且a2+b2=4时,求椭圆C的方程;
(2)求|![]() |的最大值.
|的最大值.
查看答案和解析>>
科目:高中数学 来源:2013-2013学年湖北省荆门市高二(下)期末数学试卷(文科)(解析版) 题型:解答题
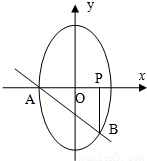 如图椭圆C的方程为
如图椭圆C的方程为 ,A是椭圆C的短轴左顶点,过A点作斜率为-1的直线交椭圆于B点,点P(1,0),且BP∥y轴,△APB的面积为
,A是椭圆C的短轴左顶点,过A点作斜率为-1的直线交椭圆于B点,点P(1,0),且BP∥y轴,△APB的面积为 .
.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com