
(1)如图所示,给出两块面积相同的正三角形纸片(如图(1),图(2))要求用其中一块剪拼成一个正三棱柱模型,另一块剪拼成一个正三棱锥模型,使它们的全面积都相等,请设计一种剪拼方法,分别用虚线标示在图(1)、图(2)中,并作简要说明:

(2)(本小题为附加题)如果给出的是一块任意三角形纸片(如图(3)).要求剪拼成一个直三棱柱模型,全面积与给出的三角形的面积相等,请设计一种剪拼方法,作虚线表示在图(3)中,并作简要说明.
|
解:(1)如图(1)所示,正三角形三边中点连线折起,可拼得一个正三棱锥.
如图(2)所示,正三角形上剪出三个相同的四边形.其较长的一组邻边边长为三角形边长的 (2)如图(3)所示,分别连结三角形的内心与各顶点,得到三条线段,再以这三条线段的中点为顶点作三角形.以新作的三角形为直三棱柱的底面.过新三角形的三个顶点向原三角形三边作垂线,沿六条垂线剪下三个四边形,可以拼接成直三棱柱的上底,余下部分按虚线折起,成为一个缺上底的直三棱柱,即可得到直三棱柱模型. |
|
分析:剪拼成正三棱锥的问题可借助正四面体的“侧面展开图”来考虑.正四面体(特殊的正三棱锥)的四个面是全等的正三角形,沿三条棱剪开后,“摊平”,正好拼成一个大正三角形,因此沿正三角形纸片的三条中位线折叠,就可得到一个正三棱锥的模型. 剪拼所得正三棱柱底面是正三角形,方法1是参照(1)中作为底面的小正三角形旋转60°,即以正三角形纸片的内心与各顶点连线的中点为顶点剪得的正三角形为棱柱的一个底面(面积为纸片的 解题心得:将一个正三角形剪拼成正三棱柱模型还有以下方法(如图):用正三角形纸片的一条中位线截得的小三角形为棱柱一个底面,由相应的两个中点向第三条作垂线截得一个矩形,将此矩形“横向”等分成三个小矩形(其一边长等于底面边长)作为棱柱的三个侧面,纸片剩下的两个小的直角三角形正好又拼成棱柱的另一个底.
|


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
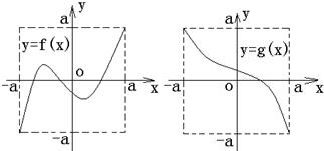 10、定义域和值域均为[-a,a](常数a>0)的函数y=f(x)和y=g(x)的图象如图所示,给出下列四个命题:
10、定义域和值域均为[-a,a](常数a>0)的函数y=f(x)和y=g(x)的图象如图所示,给出下列四个命题:查看答案和解析>>
科目:高中数学 来源: 题型:
 我们把离心率为e=
我们把离心率为e=
| ||
| 2 |
| x2 |
| a2 |
| y2 |
| b2 |
| 2y2 | ||
|
查看答案和解析>>
科目:高中数学 来源: 题型:
 已知函数f(x)的导函数f'(x)的图象如图所示,给出以下结论:
已知函数f(x)的导函数f'(x)的图象如图所示,给出以下结论:查看答案和解析>>
科目:高中数学 来源: 题型:
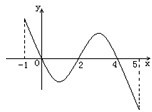 已知函数f(x)的定义域为[-1,5],部分对应值如下表,f(x)的导函数y=f′(x)的图象如图所示.给出关于f(x)的下列命题:
已知函数f(x)的定义域为[-1,5],部分对应值如下表,f(x)的导函数y=f′(x)的图象如图所示.给出关于f(x)的下列命题:| x | -1 | 0 | 4 | 5 |
| f(x) | 1 | 2 | 2 | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com