
已知定义在![]() 上的奇函数
上的奇函数![]() 在
在![]() 处取得极值.
处取得极值.
(Ⅰ)求函数![]() 的解析式;
的解析式;
(Ⅱ)试证:对于区间![]() 上任意两个自变量的值
上任意两个自变量的值![]() ,都有
,都有![]() 成立;
成立;
(Ⅲ)若过点![]() 可作曲线
可作曲线![]() 的三条切线,试求点P对应平面区域的面积.
的三条切线,试求点P对应平面区域的面积.
(Ⅰ) ![]() (Ⅲ)8
(Ⅲ)8
(I)由题意![]() ,∴
,∴![]() ,
,
∴![]() ,又
,又![]() ,
,
即![]()
解得![]() .
.
∴![]() ------------------------------------------------4分
------------------------------------------------4分
(II)∵![]() ,
,![]() ,
,
当![]() 时,
时,![]() ,故
,故![]() 在区间[-1,1]上为减函数,
在区间[-1,1]上为减函数,
∴![]()
对于区间[-1,1]上任意两个自变量的值![]() ,
,
∴![]() -------------------------------9分
-------------------------------9分
(III)设切点为![]() ,则点M的坐标满足
,则点M的坐标满足![]()
因![]() ,故切线
,故切线![]() 的方程为:
的方程为:
![]() ,
,
∵![]() ,∴
,∴![]()
整理得![]() .
.
∵若过点![]() 可作曲线
可作曲线![]() 的三条切线,
的三条切线,
∴关于![]() 方程
方程![]() 有三个实根.
有三个实根.
设![]() ,则
,则
![]() ,
,
由![]() ,得
,得![]() 或
或![]() .
.
由对称性,先考虑![]()
∵![]() 在
在![]() ,
,![]() 上单调递增,在
上单调递增,在![]() 上单调递减.
上单调递减.
∴函数![]() 的极值点为
的极值点为![]() ,或
,或![]()
∴关于![]() 方程
方程![]() 有三个实根的充要条件是
有三个实根的充要条件是
![]() ,解得
,解得![]() .
.
故![]() 时,点P对应平面区域的面积
时,点P对应平面区域的面积![]()
故![]() 时,所求点P对应平面区域的面积为
时,所求点P对应平面区域的面积为![]() ,即8.
,即8.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
A、(
| ||
B、(
| ||
C、[1,
| ||
D、(-∞,
|
查看答案和解析>>
科目:高中数学 来源:2010年新课标版广东省遂溪县高一数学必修一(函数、导数、方程与不等式)单元测试 题型:解答题
已知定义在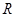 上的奇函数
上的奇函数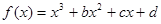 在
在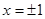 处取得极值.
处取得极值.
(Ⅰ)求函数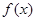 的解析式;
的解析式;
(Ⅱ)试证:对于区间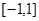 上任意两个自变量的值
上任意两个自变量的值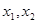 ,都有
,都有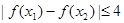 成立;
成立;
(Ⅲ)若过点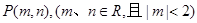 可作曲线
可作曲线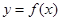 的三条切线,试求点P对应平面区域的面积.
的三条切线,试求点P对应平面区域的面积.
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
A.(
| B.(
| C.[1,
| D.(-∞,
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com