
已知函数
(1)求 的单调减区间;
的单调减区间;
(2)若方程 有三个不同的实根,求
有三个不同的实根,求 的取值范围;
的取值范围;
(3)若 在区间[-2,2]上的最大值为20,求它在该区间上的最小值.
在区间[-2,2]上的最大值为20,求它在该区间上的最小值.
解:(1)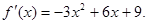 令
令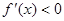 ,解得
,解得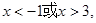 ……………2分
……………2分
所以函数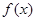 的单调递减区间为
的单调递减区间为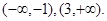 …………………3分
…………………3分
(2)由(1)可知,函数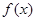 的单调递减区间为
的单调递减区间为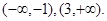 ,函数
,函数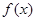 的单调递增区间为
的单调递增区间为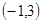 ,所以
,所以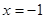 是极小值点,
是极小值点,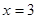 是极大值点,
…………………………4分
是极大值点,
…………………………4分
所以,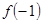 是极小值且
是极小值且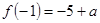 ,
,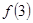 是极大值且
是极大值且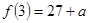 …………5分
…………5分
方程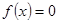 有三个不同的实根,即
有三个不同的实根,即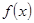 的图象与
的图象与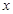 轴有三个交点,需满足
轴有三个交点,需满足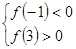
 解得:
解得: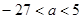 …………………………7分
…………………………7分
(3)因为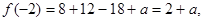
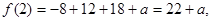
所以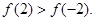 …………………………………8分
…………………………………8分
因为在(-1,3)上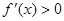 ,所以
,所以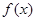 在[-1,2]上单调递增,又由于
在[-1,2]上单调递增,又由于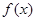 在[-2,-1]上单调递减,因此
在[-2,-1]上单调递减,因此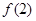 和
和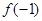 分别是
分别是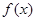 在区间
在区间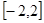 上的最大值和最小值. …… 10分
上的最大值和最小值. …… 10分
于是有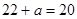 ,解得
,解得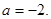 ……………………………………11分
……………………………………11分
故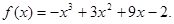 因此
因此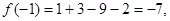
即函数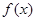 在区间
在区间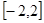 上的最小值为-7.
……………………………………12分
上的最小值为-7.
……………………………………12分
【解析】略


 通城学典默写能手系列答案
通城学典默写能手系列答案科目:高中数学 来源:2015届山东省高一6月月考数学试卷(解析版) 题型:解答题
已知函数
(1)求 的最小正周期及
的最小正周期及 取得最大值时x的集合;
取得最大值时x的集合;
(2)在平面直角坐标系中画出函数 在
在 上的图象.
上的图象.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年贵州省五校高三第四次联考数学理卷 题型:解答题
(本小题满分12分)
已知函数 ,
,
(1)求 的单调区间;
的单调区间;
(2)若对任意的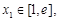 ,都存在
,都存在 ,使得
,使得 ,求
,求 的取值范围。
的取值范围。
查看答案和解析>>
科目:高中数学 来源:2010年河南省焦作市高一下学期数学必修4水平测试 题型:解答题
(10分)已知函数 .
.
(1)求 的最小正周期;
的最小正周期;
(2)求 在区间
在区间 上的最大值和最小值以及取得最大值、最小值时x的值.
上的最大值和最小值以及取得最大值、最小值时x的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com