
 .
. 时,判断
时,判断 的奇偶性,并说明理由;
的奇偶性,并说明理由; 时,若
时,若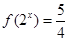 ,求
,求 的值;
的值; ,且对任何
,且对任何 不等式
不等式 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围. 既不是奇函数,也不是偶函数;(Ⅱ)
既不是奇函数,也不是偶函数;(Ⅱ)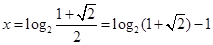 或
或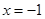 ;
;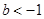 时,
时, 的取值范围是
的取值范围是 ;当
;当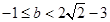 时,
时, 的取值范围是
的取值范围是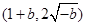 ;当
;当 时,
时, 的取值范围是
的取值范围是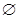 .
. 时,
时,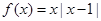 ,从解析式可以看出它既不是奇函数,也不是偶函数.对既不是奇函数,也不是偶函数的函数,一般取两个特殊值说明.
,从解析式可以看出它既不是奇函数,也不是偶函数.对既不是奇函数,也不是偶函数的函数,一般取两个特殊值说明. 时,
时,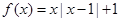 , 由
, 由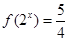 得
得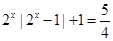 ,这是一个含有绝对值符号的不等式,对这种不等式,一般先分情况去绝对值符号.这又是一个含有指数式的不等式,对这种不等式,一般将指数式看作一个整体,先求出指数式的值,然后再利用指数式求出
,这是一个含有绝对值符号的不等式,对这种不等式,一般先分情况去绝对值符号.这又是一个含有指数式的不等式,对这种不等式,一般将指数式看作一个整体,先求出指数式的值,然后再利用指数式求出 的值.
的值. ,故首先考虑
,故首先考虑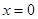 的情况. 易得
的情况. 易得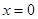 时,
时, 取任意实数,不等式
取任意实数,不等式 恒成立.
恒成立. ,此时原不等式变为
,此时原不等式变为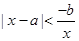 ;即
;即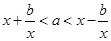 ,这时应满足:
,这时应满足: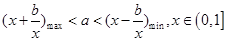 ,所以接下来就求
,所以接下来就求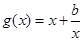 的最大值和
的最大值和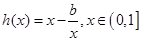 的最小值.在求这个最大值和最小值时,因数还有一个参数
的最小值.在求这个最大值和最小值时,因数还有一个参数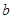 ,所以又需要对
,所以又需要对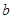 进行讨论.
进行讨论. 时,
时,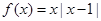 既不是奇函数也不是偶函数
既不是奇函数也不是偶函数 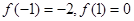 ,∴
,∴
 既不是奇函数,也不是偶函数 3分
既不是奇函数,也不是偶函数 3分 时,
时,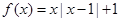 , 由
, 由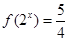 得
得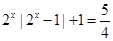
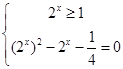 或
或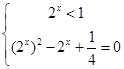

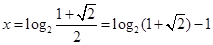 或
或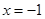 8分
8分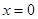 时,
时, 取任意实数,不等式
取任意实数,不等式 恒成立,
恒成立,  ,此时原不等式变为
,此时原不等式变为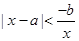 ;即
;即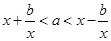
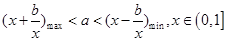
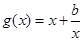 在
在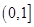 上单调递增,所以
上单调递增,所以 ;
; 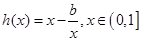
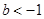 时,在
时,在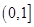 上
上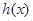 单调递减,
单调递减,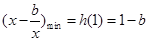 ,又
,又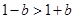 ,
,  的取值范围是
的取值范围是
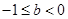 ,在
,在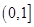 上,
上,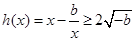 ,
, 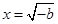 时,
时,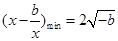 ,此时要使
,此时要使 存在,
存在,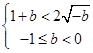 即
即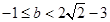 ,此时
,此时 的取值范围是
的取值范围是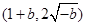
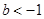 时,
时, 的取值范围是
的取值范围是 ;
; 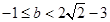 时,
时, 的取值范围是
的取值范围是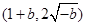 ;
;  时,
时, 的取值范围是
的取值范围是 13分
13分

 天天向上一本好卷系列答案
天天向上一本好卷系列答案科目:高中数学 来源:不详 题型:解答题
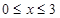 时,f(x)=
时,f(x)=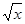 -1.
-1.
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
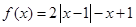 .
.
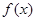 的图像;
的图像;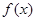 的图像回答下列问题:
的图像回答下列问题: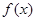 的单调区间;
的单调区间;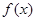 的值域;
的值域;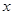 的方程
的方程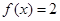 在区间
在区间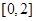 上解的个数.
上解的个数.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.增函数且最小值是-5 | B.增函数且最大值是-5 |
| C.减函数且最大值是-5 | D.减函数且最小值是-5 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
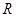 上的函数
上的函数 ,有如下四个命题:
,有如下四个命题: ,则函数
,则函数 是奇函数;②若
是奇函数;②若 则函数
则函数 不是偶函数;
不是偶函数; 则函数
则函数 是
是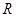 上的增函数;④若
上的增函数;④若 则函数
则函数 不是
不是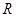 上的减函数.其中正确的命题有______________.(写出你认为正确的所有命题的序号).
上的减函数.其中正确的命题有______________.(写出你认为正确的所有命题的序号).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com