解:(1))a
1=2,a
2=2λ+2,a
3=λa
2+4=2λ
2+2λ+4(1分)
①若数列{a
n}为等}为等差数列,则得λ
2-λ+1=0由△=12-4=-3<0知方程无实根,故不存在实数λ,(3分)
②若数列{a
n}为等比数列得(2+2λ)
2=2(2λ
2+2λ+4),解得λ=1
则a
n+1=a
n+2
na
2-a
1=2
a
3-a
2=2
2…
a
n-a
n-1=2
n-1由累加法得:a
n-a
1=2+2
2+…+2
n-1=2
n-2
解得a
n=2
n(n≥2)
显然,当n=1时也适合,故a
n=2
n(n∈N*).
故存在实数λ=1,使得数列{an}为等比数列,其通项公式为a
n=2
n(6分)
(2)λ=1时由(1)可得,
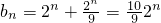
,
∴
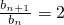
∴数列{b
n}是等比数列
(3))①当λ=1时,a
n=2
n,
由等比数列的求和公式可得,
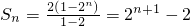
(7分)
②当λ=2时,构造等差数列 {

}求解,,③当λ≠1且λ≠2时,构造等比数列 {
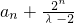
}求解.
分析:(1)a
1=2,a
2=2λ+2,a
3=λa
2+4=2λ
2+2λ+4.分两种情况讨论①数列{a
n}为等差数列,得λ
2-λ+1=0由△=12-4=-3<0知方程无实根,故不存在实数λ,②若数列{a
n}为等比数列得(2+2λ)
2=2(2λ
2+2λ+4),解得λ=1,a
n+1=a
n+2
n解得a
n=2
n,故存在实数λ=1,使得数列{a
n}为等比数列.
(2)λ=1时由(1)可得,
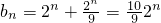
,容易证明
(3)①当λ=1时,转化为等比数列求解.②当λ=2时,构造等差数列 {

}求解,,③当λ≠1且λ≠2时,构造等比数列 {
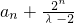
}求解.
点评:本题是一道数列综合题,情景熟悉,貌似简单,入手也不难,但综合程度之高令人叹为观止.无论是分类讨论的思想,还是反证推理、求数列通项和数列求和都考查得淋漓尽致,累加法和待定系数法求数列的通项、错位相减法和分组求和法求数列的前n项和,几乎数列的所有知识和方法都熔于一炉.

 ×2n,证明数列{bn}是等比数列;
×2n,证明数列{bn}是等比数列;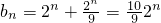 ,
,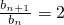
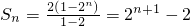 (7分)
(7分) }求解,,③当λ≠1且λ≠2时,构造等比数列 {
}求解,,③当λ≠1且λ≠2时,构造等比数列 {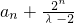 }求解.
}求解.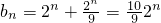 ,容易证明
,容易证明 }求解,,③当λ≠1且λ≠2时,构造等比数列 {
}求解,,③当λ≠1且λ≠2时,构造等比数列 {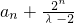 }求解.
}求解.
