


科目:高中数学 来源: 题型:
| A、竖直向上发射的信号弹,从发射到落回地面,信号弹的高度与时间的关系(不计空气阻力). | B、我国人口年自然增长率为1%,这样我国人口总数随年份的变化关系. | C、如果某人ts内骑车行进了1km,那么此人骑车的平均速度v与时间t的函数关系. | D、信件的邮资与其重量间的函数关系. |
查看答案和解析>>
科目:高中数学 来源:2006-2007年上学期许昌市高三数学四校联考(附答案) 题型:044
已知函数f(x)=loga(a-kax)(a>0,且a≠1,k∈R).
若f(x)的图像关于直线y=x对称,且f(2)=-2loga2,求a的值.
当0<a<1时,若f(x)在[1,+∞)内恒有意义,求k的取值范围.
查看答案和解析>>
科目:高中数学 来源:2008-2009学年重庆八中高三(上)第一次月考数学试卷(文科)(解析版) 题型:选择题
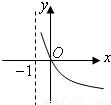
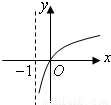
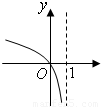
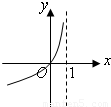
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com