Question

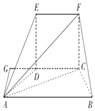
【题目】（题文）如图，在五面体ABCDEF中，四边形EDCF是正方形，．

(1)证明：；

(2)已知四边形ABCD是等腰梯形，且，求五面体ABCDEF的体积.

Answer 1

【答案】(1)见解析；（2）见解析.

【解析】

分析：(1)先根据线面垂直判定定理得平面.，即得. 再根据平行关系得结论，(2)先分割. 过作，根据线面垂直判定定理得平面，则是四棱锥的高.由（1）可得平面,则是三棱锥的高.最后根据锥体体积公式求体积.

详解：（1）证明：由已知的,,、 平面，且∩,

所以平面.

又 平面,所以.

又因为//,所以.

（2）解：连结、,则.

过作交于，又因为平面，所以，且∩，

所以平面，则是四棱锥的高.

因为四边形是底角为的等腰梯形，,

所以，,.

因为平面，//，所以平面,则是三棱锥的高.

所以，

所以.

点睛:空间几何体体积问题的常见类型及解题策略

(1)若所给定的几何体是可直接用公式求解的柱体、锥体或台体，则可直接利用公式进行求解．

(2)若所给定的几何体的体积不能直接利用公式得出，则常用转换法、分割法、补形法等方法进行求解．

(3)若以三视图的形式给出几何体，则应先根据三视图得到几何体的直观图，然后根据条件求解．