
【题目】已知二次函数 ![]() 的最小值为0,不等式
的最小值为0,不等式 ![]() 的解集为
的解集为 ![]() .
.
(1)求集合 ![]() ;
;
(2)设集合 ![]() ,若集合
,若集合 ![]() 是集合
是集合 ![]() 的子集,求
的子集,求 ![]() 的取值范围.
的取值范围.
【答案】
(1)解:由二次函数 ![]() 的最小值是0得:
的最小值是0得: ![]() ,
, ![]() ,所以集合
,所以集合 ![]()
(2)解:当 ![]() 时,集合
时,集合 ![]() 符合题意;当
符合题意;当 ![]() 时,集合
时,集合 ![]() ,∴
,∴ ![]() ,∴
,∴ ![]() .综上
.综上 ![]() 的取值范围是
的取值范围是 ![]()
【解析】(1)利用二次函数的最小值求得b的值,再解得到的一元二次不等式即可得到集合A;(2)利用集合A与集合B的关系可以得知集合B包含于集合A,同时注意考虑集合B为空集时集合A,B的关系仍成立.
【考点精析】本题主要考查了解一元二次不等式的相关知识点,需要掌握求一元二次不等式![]()
![]() 解集的步骤:一化:化二次项前的系数为正数;二判:判断对应方程的根;三求:求对应方程的根;四画:画出对应函数的图象;五解集:根据图象写出不等式的解集;规律:当二次项系数为正时,小于取中间,大于取两边才能正确解答此题.
解集的步骤:一化:化二次项前的系数为正数;二判:判断对应方程的根;三求:求对应方程的根;四画:画出对应函数的图象;五解集:根据图象写出不等式的解集;规律:当二次项系数为正时,小于取中间,大于取两边才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】设数列{an}的前n项和为Sn , 若点 ![]() 在函数f(x)=﹣x+c的图象上运动,其中c是与x无关的常数,且a1=3.
在函数f(x)=﹣x+c的图象上运动,其中c是与x无关的常数,且a1=3.
(1)求数列{an}的通项公式;
(2)记 ![]() ,求数列{bn}的前n项和Tn的最小值.
,求数列{bn}的前n项和Tn的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是数列
是数列![]() 的前n项和,
的前n项和,![]() ,且
,且![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)对于正整数![]() ,已知
,已知![]() 成等差数列,求正整数
成等差数列,求正整数![]() 的值;
的值;
(3)设数列![]() 前n项和是
前n项和是![]() ,且满足:对任意的正整数n,都有等式
,且满足:对任意的正整数n,都有等式![]() 成立.求满足等式
成立.求满足等式![]() 的所有正整数n.
的所有正整数n.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】4月16日摩拜单车进驻大连市旅顺口区,绿色出行引领时尚,旅顺口区对市民进行“经常使用共享单车与年龄关系”的调查统计,若将单车用户按照年龄分为“年轻人”(20岁~39岁)和“非年轻人”(19岁及以下或者40岁及以上)两类,抽取一个容量为200的样本,将一周内使用的次数为6次或6次以上的称为“经常使用单车用户”。使用次数为5次或不足5次的称为“不常使用单车用户”,已知“经常使用单车用户”有120人,其中 ![]() 是“年轻人”,已知“不常使用单车用户”中有
是“年轻人”,已知“不常使用单车用户”中有 ![]() 是“年轻人”.
是“年轻人”.
(1)请你根据已知的数据,填写下列 ![]() 列联表:
列联表:
年轻人 | 非年轻人 | 合计 | |
经常使用单车用户 | |||
不常使用单车用户 | |||
合计 |
(2)请根据(1)中的列联表,计算 ![]() 值并判断能否有
值并判断能否有 ![]() 的把握认为经常使用共享单车与年龄有关?
的把握认为经常使用共享单车与年龄有关?
(附: ![]()
当 ![]() 时,有
时,有 ![]() 的把握说事件
的把握说事件 ![]() 与
与 ![]() 有关;当
有关;当 ![]() 时,有
时,有 ![]() 的把握说事件
的把握说事件 ![]() 与
与 ![]() 有关;当
有关;当 ![]() 时,认为事件
时,认为事件 ![]() 与
与 ![]() 是无关的)
是无关的)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一段时间内有2000辆车通过高速公路上的某处,现随机抽取其中的200辆进行车速统计,统计结果如右面的频率分布直方图所示.若该处高速公路规定正常行驶速度为90km/h~120 km/h,试估计2000辆车中,在这段时间内以正常速度通过该处的汽车约有( )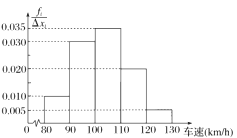
A.30辆
B.1700辆
C.170辆
D.300辆
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知全集U=R,集合A={x|x2﹣x﹣6≤0}, ![]() ,那么集合A∩(UB)=( )
,那么集合A∩(UB)=( )
A.[﹣2,4)
B.(﹣1,3]
C.[﹣2,﹣1]
D.[﹣1,3]
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com