练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】长方体ABCD﹣A1B1C1D1中AB=AA1=2，AD=1，E为CC1的中点，则异面直线BC1与AE所成角的余弦值为（ ）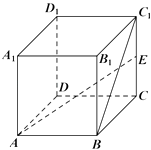

    A.
    B.
    C.
    D.

    【答案】B
    【解析】解析：建立坐标系如图．则A（1，0，0），E（0，2，1），B（1，2，0），C1（0，2，2）．
    =（﹣1，0，2），A=（﹣1，2，1），
    cos＜ ＞═ ．
    所以异面直线BC1与AE所成角的余弦值为 ．
    故选B

    【考点精析】掌握异面直线及其所成的角是解答本题的根本，需要知道异面直线所成角的求法：1、平移法：在异面直线中的一条直线中选择一特殊点，作另一条的平行线；2、补形法：把空间图形补成熟悉的或完整的几何体，如正方体、平行六面体、长方体等，其目的在于容易发现两条异面直线间的关系．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】生产甲乙两种精密电子产品，用以下两种方案分别生产出甲乙产品共种，现对这两种方案生产的产品分别随机调查了各次，得到如下统计表：

    ①生产件甲产品和件乙产品

    正次品

    甲正品

    甲正品

    乙正品

    甲正品

    甲正品

    乙次品

    甲正品

    甲次品

    乙正品

    甲正品

    甲次品

    乙次品

    甲次品

    甲次品

    乙正品

    甲次品

    甲次品

    乙次品

    频 数

    ②生产件甲产品和件乙产品

    正次品

    乙正品

    乙正品

    甲正品

    乙正品

    乙正品

    甲次品

    乙正品

    乙次品

    甲正品

    乙正品

    乙次品

    甲次品

    乙次品

    乙次品

    甲正品

    乙次品

    乙次品

    甲次品

    频 数

    已知生产电子产品甲件，若为正品可盈利元，若为次品则亏损元；生产电子产品乙件，若为正品可盈利元，若为次品则亏损元．

    （I）按方案①生产件甲产品和件乙产品，求这件产品平均利润的估计值；

    （II）从方案①②中选其一，生产甲乙产品共件，欲使件产品所得总利润大于元的机会多，应选用哪个？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）是定义在R上的奇函数，且f（﹣3）=0，当x＞0时，有f（x）﹣xf′（x）＞0成立，则不等式f（x）＞0的解集是（ ）
    A.（﹣∞，﹣3）∪（0，3）
    B.（﹣∞，﹣3）∪（3，+∞）
    C.（﹣3，0）∪（0，3）
    D.（﹣3，0）∪（3，+∞）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在平面直角坐标系中，O为坐标原点，已知向量 =（﹣1，2），又点A（8，0），B（n，t），C（ksinθ，t）．
    （1）若 ⊥ ，且| |= | |，求向量 ；
    （2）若向量 与向量 共线，常数k＞0，求f（θ）=tsinθ的值域；
    （3）当（2）问中f（θ）的最大值4时，求 ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在平面直角坐标系中，已知圆经过椭圆的焦点.

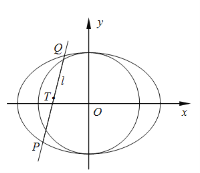
    （1）求椭圆的标准方程；

    （2）设直线交椭圆于两点，为弦的中点，，记直线的斜率分别为，当时，求的值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知曲线的极坐标方程为，在以极点为直角坐标原点，极轴为轴的正半轴建立的平面直角坐标系中，直线的参数方程为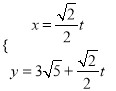（为参数）.

    （1）写出直线的普通方程与曲线的直角坐标方程；

    （2）在平面直角坐标系中，设曲线经过伸缩变换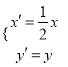： 得到曲线，若为曲线上任意一点，求点到直线的最小距离.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在直三棱柱ABC﹣A1B1C1中，点D是BC的中点．

    （1）求证：A1B∥平面ADC1；
    （2）若AB⊥AC，AB=AC=1，AA1=2，求平面ADC1与ABA1所成二面角的正弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=|x﹣1|+|x﹣a|
    （1）当a=2时，解不等式f（x）≥4．
    （2）若不等式f（x）≥2a恒成立，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在如图所示的几何体中，四边形ABCD是菱形，ADNM是矩形，平面ADNM⊥平面ABCD，∠DAB=60°，AD=2，AM=1，E为AB的中点．

    （Ⅰ）求证：AN∥平面MEC；

    （Ⅱ）在线段AM上是否存在点P，使二面角P﹣EC﹣D的大小为 ？若存在，求出AP的长h；若不存在，请说明理由．

    查看答案和解析>>

    同步练习册答案