
【题目】已知双曲线![]() 的左、右焦点分别为F1,F2,以线段F1F2为直径的圆与双曲线的渐近线在第一象限的交点为P,且P满足|PF1|﹣|PF2|=2b,则C的离心率e满足( )
的左、右焦点分别为F1,F2,以线段F1F2为直径的圆与双曲线的渐近线在第一象限的交点为P,且P满足|PF1|﹣|PF2|=2b,则C的离心率e满足( )
A. e2﹣3e+1=0B. e4﹣3e2+1=0C. e2﹣e﹣1=0D. e4﹣e2﹣1=0
 作业辅导系列答案
作业辅导系列答案科目:高中数学 来源: 题型:
【题目】若函数y=f(x)在区间D上是增函数,且函数y=![]() 在区间D上是减函数,则称函数f(x)是区间D上的“H函数”.对于命题:
在区间D上是减函数,则称函数f(x)是区间D上的“H函数”.对于命题:
①函数f(x)=-x+![]() 是区间(0,1)上的“H函数”;
是区间(0,1)上的“H函数”;
②函数g(x)=![]() 是区间(0,1)上的“H函数”.下列判断正确的是( )
是区间(0,1)上的“H函数”.下列判断正确的是( )
A. ![]() 和
和![]() 均为真命题 B.
均为真命题 B. ![]() 为真命题,
为真命题,![]() 为假命题
为假命题
C. ![]() 为假命题,
为假命题,![]() 为真命题 D.
为真命题 D. ![]() 和
和![]() 均为假命题
均为假命题
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】李明自主创业,在网上经营一家水果店,销售的水果中有草莓、京白梨、西瓜、桃,价格依次为60元/盒、65元/盒、80元/盒、90元/盒.为增加销量,李明对这四种水果进行促销:一次购买水果的总价达到120元,顾客就少付x元.每笔订单顾客网上支付成功后,李明会得到支付款的80%.
①当x=10时,顾客一次购买草莓和西瓜各1盒,需要支付__________元;
②在促销活动中,为保证李明每笔订单得到的金额均不低于促销前总价的七折,则x的最大值为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义首项为1且公比为正数的等比数列为“M-数列”.
(1)已知等比数列{an}满足:![]() ,求证:数列{an}为“M-数列”;
,求证:数列{an}为“M-数列”;
(2)已知数列{bn}满足:![]() ,其中Sn为数列{bn}的前n项和.
,其中Sn为数列{bn}的前n项和.
①求数列{bn}的通项公式;
②设m为正整数,若存在“M-数列”{cn}![]() ,对任意正整数k,当k≤m时,都有
,对任意正整数k,当k≤m时,都有![]() 成立,求m的最大值.
成立,求m的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《中华人民共和国道路交通安全法》第47条的相关规定:机动车行经人行道时,应当减速慢行;遇行人正在通过人行道,应当停车让行,俗称“礼让斑马线”, 《中华人民共和国道路交通安全法》第90条规定:对不礼让行人的驾驶员处以扣3分,罚款50元的处罚.下表是某市一主干路口监控设备所抓拍的5个月内驾驶员“礼让斑马线”行为统计数据:
月份 | 1 | 2 | 3 | 4 | 5 |
违章驾驶员人数 | 120 | 105 | 100 | 90 | 85 |
(1)请利用所给数据求违章人数![]() 与月份
与月份![]() 之间的回归直线方程
之间的回归直线方程![]() ;
;
(2)预测该路口9月份的不“礼让斑马线”违章驾驶员人数.
参考公式:  ,
, ![]() .
.
参考数据: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=![]() ,若x1,x2∈R,且x1≠x2,使得f(x1)=f(x2),则实数a的取值范围是( )
,若x1,x2∈R,且x1≠x2,使得f(x1)=f(x2),则实数a的取值范围是( )
A. [2,3]∪(﹣∞,﹣5]B. (﹣∞,2)∪(3,5)
C. [2,3]D. [5,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
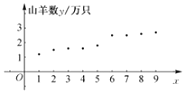
【题目】某县畜牧技术员张三和李四9年来一直对该县山羊养殖业的规模进行跟踪调查,张三提供了该县某山羊养殖场年养殖数量![]() 单位:万只
单位:万只![]() 与相应年份
与相应年份![]() 序号
序号![]() 的数据表和散点图
的数据表和散点图![]() 如图所示
如图所示![]() ,根据散点图,发现y与x有较强的线性相关关系,李四提供了该县山羊养殖场的个数
,根据散点图,发现y与x有较强的线性相关关系,李四提供了该县山羊养殖场的个数![]() 单位:个
单位:个![]() 关于x的回归方程
关于x的回归方程![]() .
.
年份序号x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
年养殖山羊 |
|
|
|
|
|
|
|
|
|
![]() 根据表中的数据和所给统计量,求y关于x的线性回归方程
根据表中的数据和所给统计量,求y关于x的线性回归方程![]() 参考统计量:
参考统计量:![]() ,
,![]() ;
;
![]() 试估计:
试估计:![]() 该县第一年养殖山羊多少万只
该县第一年养殖山羊多少万只
![]() 到第几年,该县山羊养殖的数量与第一年相比缩小了?
到第几年,该县山羊养殖的数量与第一年相比缩小了?
附:对于一组数据![]() ,
,![]() ,
,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为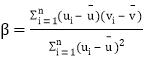 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解某品种一批树苗生长情况,在该批树苗中随机抽取了容量为120的样本,测量树苗高度(单位:cm),经统计,其高度均在区间[19,31]内,将其按[19,21),[21,23),[23,25),[25,27),[27,29),[29,31]分成6组,制成如图所示的频率分布直方图.其中高度为27 cm及以上的树苗为优质树苗.
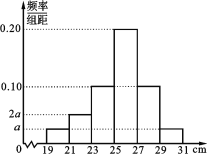
(1)求图中a的值;
(2)已知所抽取的这120棵树苗来自于A,B两个试验区,部分数据如下列联表:
A试验区 | B试验区 | 合计 | |
优质树苗 | 20 | ||
非优质树苗 | 60 | ||
合计 |
将列联表补充完整,并判断是否有99.9%的把握认为优质树苗与A,B两个试验区有关系,并说明理由;
(3)用样本估计总体,若从这批树苗中随机抽取4棵,其中优质树苗的棵数为X,求X的分布列和数学期望EX.
下面的临界值表仅供参考:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式:![]() ,其中
,其中![]() .)
.)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com