
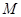 是满足下列性质的函数
是满足下列性质的函数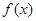 的全体:在定义域内存在
的全体:在定义域内存在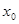 ,使得
,使得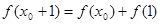 成立。
成立。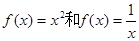 是否属于集合
是否属于集合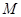 ?说明理由;
?说明理由;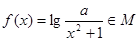 ,求实数
,求实数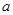 的取值范围.
的取值范围.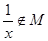 ;(Ⅱ)a
;(Ⅱ)a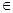 [3-
[3-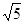 ,3+
,3+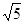 ];
]; 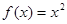 时,由
时,由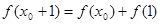 有:
有: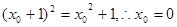 ,即
,即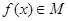 3分
3分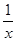 的定义域为
的定义域为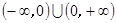 ,
,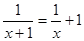 ,整理得x
,整理得x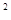 +x+1=0,△=-3<0,
+x+1=0,△=-3<0,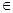
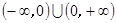 使得f(x+1)=f(x)+f(1)成立,所以f(x)=
使得f(x+1)=f(x)+f(1)成立,所以f(x)=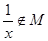 ;…… 6分
;…… 6分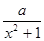 的定义域为R,f(1)=lg
的定义域为R,f(1)=lg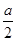 ,a>0, ..7分
,a>0, ..7分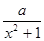
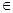 M,则存在x
M,则存在x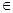 R使得lg
R使得lg =lg
=lg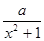 +lg
+lg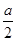 ,
,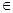 R使得(a-2)x
R使得(a-2)x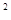 +2ax+(2a-2)=0. 8分
+2ax+(2a-2)=0. 8分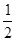 ,满足条件; 10分
,满足条件; 10分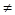 0即a
0即a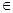
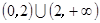 时,令△≥0, 12分
时,令△≥0, 12分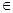
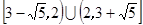 , 13分
, 13分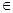 [3-
[3-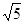 ,3+
,3+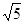 ]; 14分
]; 14分

 阅读快车系列答案
阅读快车系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com