
【题目】如图所示,底面为菱形的直四棱柱![]() 被过三点
被过三点![]() 的平面截去一个三棱锥
的平面截去一个三棱锥![]() (图一)得几何体
(图一)得几何体![]() (图二),E为
(图二),E为![]() 的中点.
的中点.
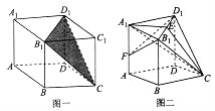
(1)点F为棱![]() 上的动点,试问平面
上的动点,试问平面![]() 与平面
与平面![]() 是否垂直?请说明理由;
是否垂直?请说明理由;
(2)设![]() ,当点F为
,当点F为![]() 中点时,求锐二面角
中点时,求锐二面角![]() 的余弦值.
的余弦值.
【答案】(1)见解析;(2)![]()
【解析】
(1)利用直四棱柱的几何特征可知![]() ,
,![]() B1D1⊥平面CEA1,从而平面
B1D1⊥平面CEA1,从而平面![]() 平面CEA1 ;(2) 分别以
平面CEA1 ;(2) 分别以![]() 所在直线为
所在直线为![]() 轴的正方向,建立空间直角坐标系,求出平面
轴的正方向,建立空间直角坐标系,求出平面![]() 与平面F
与平面F![]() 的法向量,代入公式即可得到锐二面角
的法向量,代入公式即可得到锐二面角![]() 的余弦值.
的余弦值.
(1)平面![]() 平面
平面![]() ,证明如下:
,证明如下:
连接AC,BD相交于点O,
因为底面ABCD为菱形,所以AC⊥BD,
又因为直四棱柱上下底面全等,
所以由AC⊥BD得![]() ,
,
又因为CB=CD,![]() ,
,
所以CB1=CD1.
因为E为B1D1的中点,所以![]() ,
,
又![]() ,所以B1D1⊥平面CEA1,
,所以B1D1⊥平面CEA1,
又因为![]() 平面
平面![]() ,
,
所以平面![]() 平面CEA1.
平面CEA1.
(2)连接OE,易知OE⊥平面ABCD,所以OB,OC,OE两两互相垂直,
所以分别以![]() 所在直线为
所在直线为![]() 轴的正方向,建立空间直角坐标系,如图所示,
轴的正方向,建立空间直角坐标系,如图所示,
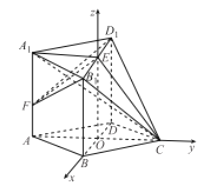
则O(0,0,0),![]() .(7分)
.(7分)
设平面![]() 的法向量为
的法向量为![]() ,则
,则
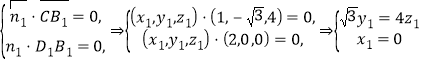 ,
,
令![]()
所以![]() .
.
同理设平面F![]() 的法向量为
的法向量为![]() ,则
,则
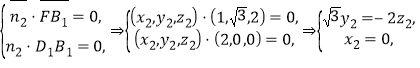 ,
,
令![]() .
.
所以![]() ,
,
所以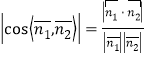
![]() ,
,
所以所求的锐二面角![]() 的余弦值为
的余弦值为![]()


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】如图,正方体![]() 的棱长为1,P,Q分别是线段
的棱长为1,P,Q分别是线段![]() 和
和![]() 上的动点,且满足
上的动点,且满足![]() ,则下列命题错误的是( )
,则下列命题错误的是( )

A.存在P,Q的某一位置,使![]()
B.![]() 的面积为定值
的面积为定值
C.当![]() 时,直线
时,直线![]() 与
与![]() 是异面直线
是异面直线
D.无论P,Q运动到任何位置,均有![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代著名的数学家刘徽著有《海岛算经》.内有一篇:“今有望海岛,立两表齐、高三丈,前后相去千步,今后表与前表相直,从前表却行百二十三步,人目著地望岛峰,与表末参合.从后表却行百二十七步,人目著地取望岛峰,亦与表末参合.问岛高及去表各几何?”(参考译文:假设测量海岛,立两根标杆,高均为5步,前后相距1000步,令前后两根标杆的底部和岛的底部在同一水平直线上,从前标杆退行123步,人的视线从地面(人的高度忽略不计)过标杆顶恰好观测到岛峰,从后标杆退行127步,人的视线从地面过标杆顶恰好观测到岛峰,问岛高多少?岛与前标杆相距多远?)(丈、步为古时计量单位,三丈=5步).则海岛高度为
A. 1055步 B. 1255步 C. 1550步 D. 2255步
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的前n项和为
的前n项和为![]() ,且
,且![]() (
(![]() ).
).
(1)求![]() ;
;
(2)设函数 ,
,![]() (
(![]() ),求数列
),求数列![]() 的前n项和
的前n项和![]() ;
;
(3)设![]() 为实数,对满足
为实数,对满足![]() 且
且![]() 的任意正整数m,n,k,不等式
的任意正整数m,n,k,不等式![]()
![]() 恒成立,试求实数
恒成立,试求实数![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】假设关于某种设备的使用年限![]() (年)与所支出的维修费用
(年)与所支出的维修费用![]() (万元)有如下统计:
(万元)有如下统计:
| 2 | 3 | 4 | 5 | 6 |
| 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
已知![]() ,
, ![]() .
. 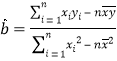 ,
, ![]()
(1)求![]() ,
, ![]() ;
;
(2)![]() 与
与![]() 具有线性相关关系,求出线性回归方程;
具有线性相关关系,求出线性回归方程;
(3)估计使用年限为10年时,维修费用约是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系中,直线l的参数方程为![]() (t为参数,
(t为参数,![]() ),以坐标原点为极点,
),以坐标原点为极点,![]() 轴正半轴为极轴,取相同的长度单位建立极坐标系,曲线C的极坐标方程为
轴正半轴为极轴,取相同的长度单位建立极坐标系,曲线C的极坐标方程为![]() .
.
(1)当![]() 时,写出直线l的普通方程及曲线C的直角坐标方程;
时,写出直线l的普通方程及曲线C的直角坐标方程;
(2)已知点![]() ,设直线l与曲线C交于A,B两点,试确定
,设直线l与曲线C交于A,B两点,试确定![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn,a1=3,an+1=2Sn+3(n∈N*).
(1)求数列{an}的通项公式;
(2)设bn=log3an,若数列![]() 的前n项和为Tn,证明:Tn<1.
的前n项和为Tn,证明:Tn<1.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com