
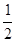
 -ax(a∈R,e为自然对数的底数).
-ax(a∈R,e为自然对数的底数).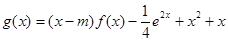 在区间(0,+
在区间(0,+ )上为增函数,求整数m的最大值.
)上为增函数,求整数m的最大值. 时,
时, 在
在 上为增函数;当
上为增函数;当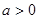 时,
时, 在
在 为减函数,在
为减函数,在 为增函数;(2)
为增函数;(2) 的最大值为1.
的最大值为1. ,由指数函数的性质可知要确定导数的正负须按
,由指数函数的性质可知要确定导数的正负须按 和
和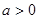 分类讨论,确定导数的符号而求出函数的单调区间;(2)函数
分类讨论,确定导数的符号而求出函数的单调区间;(2)函数 在区间(0,+
在区间(0,+ )上为增函数
)上为增函数 在
在 恒成立,分离参数m,从而将所求问题转化为求函数的最值问题,构造新函数,再用导数研究此函数的最小值即可;注意所求的m为整数这一特性.
恒成立,分离参数m,从而将所求问题转化为求函数的最值问题,构造新函数,再用导数研究此函数的最小值即可;注意所求的m为整数这一特性. ,
, ,
, 时,
时, ,所以
,所以 在
在 上为增函数; 2分
上为增函数; 2分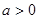 时,由
时,由 得
得 ,且当
,且当 时,
时,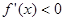 ,
, 时
时 ,
, 在
在 为减函数,在
为减函数,在 为增函数. 6分
为增函数. 6分 时,
时,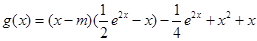 ,
, 在区间
在区间 上为增函数,
上为增函数,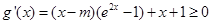 在
在 恒成立,
恒成立, 在
在 恒成立 8分
恒成立 8分 ,
,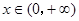 ;
; ,
,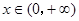 ;令
;令 ,
, ,
, ,
,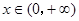 时
时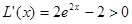 ,
, 在
在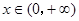 只有一个零点,设为
只有一个零点,设为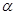 ,即
,即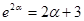 ,
, ; 9分
; 9分 时
时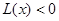 ,即
,即 ;当
;当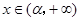 时
时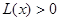 ,即
,即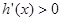 ,
, ,
,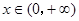 ,有最小值
,有最小值 , 10分
, 10分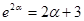 代入上式可得
代入上式可得 ,又因为
,又因为 ,所以
,所以 ,
,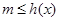 恒成立,所以
恒成立,所以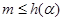 ,又因为
,又因为 为整数,
为整数, ,所以整数
,所以整数 的最大值为1. 12分
的最大值为1. 12分

 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:高中数学 来源:不详 题型:解答题
| 1 |
| 3 |
| 3 |
| 2 |
| f′(x) |
| x |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com