练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】选修4-4：坐标系与参数方程

    在直角坐标系中，曲线的参数方程为（为参数， ），曲线的参数方程为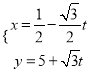（为参数），以为极点， 轴的正半轴为极轴建立坐标系.

    （1）求曲线的极坐标方程和曲线的普通方程；

    （2）射线与曲线的交点为，与曲线的交点为，求线段的长.

    【答案】（1）， ， ；（2） .

    【解析】试题分析：（1先将曲线的参数方程化为普通方程，利用可得曲线的极坐标方程，利用加减法消去参数可得曲线的普通方程；（2）通过方程组求出坐标，然后利用极径的几何意义求解即可.

    试题解析：（1）曲线的参数方程为（为参数, ），

    普通方程为（），

    极坐标方程为， ，曲线的参数方程为（为参数），

    普通方程；

    （2）， ，即；

    代入曲线的极坐标方程，可得，即，

    ∴.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知椭圆： 经过点，左右焦点分别为、，圆与直线相交所得弦长为2．　

    （Ⅰ）求椭圆的标准方程；

    （Ⅱ）设是椭圆上不在轴上的一个动点， 为坐标原点，过点作的平行线交椭圆于、两个不同的点．

    （1）试探究的值是否为一个常数？若是，求出这个常数；若不是，请说明理由．

    （2）记的面积为， 的面积为，令，求的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=（a﹣1）（ax﹣a﹣x）（0＜a＜1）．
    （1）判断f（x的奇偶性；
    （2）用定义证明f（x）为R上的增函数．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设函数f（x）=|x|，g（x）=lg（ax2﹣4x+1），若对任意x1∈R，都存在在x2∈R，使f（x1）=g（x2），则实数a的取值范围是（　　）
    A.（﹣∞，4]
    B.（0，4]
    C.（﹣4，0]
    D.[0，+∞）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】将三颗骰子各掷一次，记事件A=“三个点数都不同”，B=“至少出现一个6点”，则条件概率P（A|B），P（B|A）分别是（ ）
    A. ，
    B. ，
    C. ，
    D. ，

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】（1）求值： ． （2）求函数f(x)=的定义域．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知定义在（0， ）上的函数f（x）的导函数为f′（x），且对于任意的x∈（0， ），都有f′（x）sinx＜f（x）cosx，则（ ）
    A. f（ ）＞ f（ ）
    B.f（ ）＞f（1）
    C. f（ ）＜f（ ）
    D. f（ ）＜f（ ）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在直角△ABC中，AB⊥BC，D为BC边上异于B、C的一点，以AB为直径作⊙O，并分别交AC，AD于点E，F．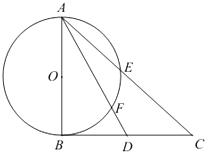

    （1）证明：C，E，F，D四点共圆；
    （2）若D为BC的中点，且AF=3，FD=1，求AE的长．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知直线l1经过两点（－1，－2）、（－1，4），直线l2经过两点（2，1）、（x，6），且l1||l2 ， 则x＝（ ）．
    A.2
    B.－2
    C.4
    D.1

    查看答案和解析>>

    同步练习册答案