
【题目】在五面体![]() 中,
中, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,平面
,平面![]() 平面
平面![]() .
.
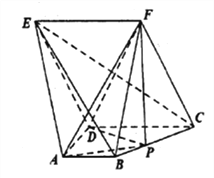
(1) 证明: 直线![]() 平面
平面![]() ;
;
(2) 已知![]() 为棱
为棱![]() 上的点,试确定
上的点,试确定![]() 点位置,使二面角
点位置,使二面角![]() 的大小为
的大小为![]() .
.
【答案】(1)见解析;(2) ![]() 点靠近
点靠近![]() 点的
点的![]() 的三等分点处.
的三等分点处.
【解析】试题分析:(1)证明一条直线垂直一个平面,只需要证明这条两个平面垂直,直线垂直两个平面的交线即可.证明CE⊥DF。∵平面CDEF⊥平面ABCD,平面CDEF∩平面ABCD=CD,CE⊥AD,即可得到直线CE⊥平面ADF.(2)根据题意,取EF的中点G,证明DA,DC,DG两两垂直.以D为原点,DA,DC,DG的方向为x,y,z轴,建立空间直角坐标系,进行计算,确定P在棱BC上的位置.
(1)∵![]() , ∴
, ∴![]()
∴四边形![]() 为菱形,∴
为菱形,∴![]()
∵平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,
∵![]() ∴
∴![]() 平面
平面![]()
∴![]() ,又∵
,又∵![]()
∴直线![]() 平面
平面![]()
(2)∵![]() ,
,
∴![]() 为正三角形,取
为正三角形,取![]() 的中点
的中点![]() ,连接
,连接![]() ,则
,则![]()
∴![]() ,
,
∵平面![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]()
∵![]() ∴
∴![]() 两两垂直
两两垂直
以![]() 为原点,
为原点, ![]() 的方向为
的方向为![]() 轴,
轴,
建立空间直角坐标系
∵![]() ,
, ![]() ,
,
∴![]()
由(1)知![]() 是平面
是平面![]() 的法向量
的法向量
∵![]() ,
,![]()
设![]() ,
,
则![]() .
.
设平面![]() 的法向量为
的法向量为![]()
∵![]() , ∴
, ∴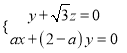 ,
,
令![]() ,则
,则![]()
∴![]()
∵二面角![]() 为
为![]() ,
,
∴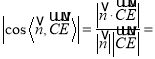
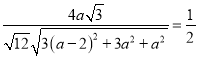 ,解得
,解得![]()
∴![]() 点靠近
点靠近![]() 点的
点的![]() 的三等分点处
的三等分点处


 口算能手系列答案
口算能手系列答案科目:高中数学 来源: 题型:
【题目】函数f(x)=sin(ωx+φ)(ω>0,|φ|< ![]() )的图象如图所示,为了得到g(x)=sinωx的图象,则只要将f(x)的图象( )
)的图象如图所示,为了得到g(x)=sinωx的图象,则只要将f(x)的图象( ) 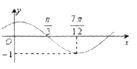
A.向左平移 ![]() 个单位长度
个单位长度
B.向右平移 ![]() 个单位长度
个单位长度
C.向右平移 ![]() 个单位长度
个单位长度
D.向左平移 ![]() 个单位长度
个单位长度
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图某综艺节目现场设有A,B,C,D四个观众席,现有由5不同颜色的马甲可供现场观众选择,同一观众席上的马甲的颜色相同,相邻观众席上的马甲的颜色不相同,则不同的安排方法种数为 . 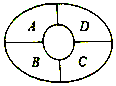
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的最小正周期为
的最小正周期为![]() .
.
(1)求函数![]() 的单调增区间;
的单调增区间;
(2)将函数![]() 的图象向左平移
的图象向左平移![]() 个单位,再向上平移1个单位,得到函数
个单位,再向上平移1个单位,得到函数![]() 的图象,若
的图象,若![]() 在
在![]() 上至少含有10个零点,求
上至少含有10个零点,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列各对函数中,相同的是( )
A.f(x)=lgx2 , g(x)=2lgx
B.f(x)=lg ![]() ,g(x)=lg(x+1)﹣lg(x﹣1)
,g(x)=lg(x+1)﹣lg(x﹣1)
C.f(u)= ![]() ,g(v)=
,g(v)= ![]()
D.f(x)=x,g(x)= ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)= ![]() x3﹣x2+ax+m,其中a>0,如果存在实数t,使f′(t)<0,则f′(t+2)f′(
x3﹣x2+ax+m,其中a>0,如果存在实数t,使f′(t)<0,则f′(t+2)f′( ![]() )的值( )
)的值( )
A.必为正数
B.必为负数
C.必为非负
D.必为非正
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在Rt△ABC中,已知A(﹣2,0),直角顶点B(0,﹣2 ![]() ),点C在x轴上. (Ⅰ)求Rt△ABC外接圆的方程;
),点C在x轴上. (Ⅰ)求Rt△ABC外接圆的方程;
(Ⅱ)求过点(﹣4,0)且与Rt△ABC外接圆相切的直线的方程.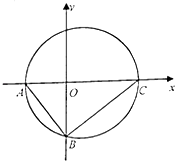
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com